题目内容
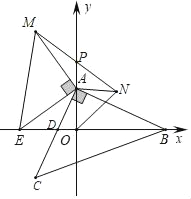
【题目】在![]() 中,
中,![]() ,过点
,过点![]() 作
作![]() 交射线
交射线![]() 于点
于点![]() ,若
,若![]() 是等腰三角形,则
是等腰三角形,则![]() 的大小为_________度.
的大小为_________度.
【答案】![]() 或
或![]()
【解析】
分两种情况考虑,∠BAC为锐角时,由AB=BD得∠D=∠DAB,由AB=AC得∠ABC=∠C,根据三角形外角性质可推出∠C=2∠D,根据直角三角形的两锐角互余可得∠C=60![]() ;同理,∠BAC为钝角时,可推出∠ADC=2∠C,根据直角三角形的两锐角互余可得∠C=30
;同理,∠BAC为钝角时,可推出∠ADC=2∠C,根据直角三角形的两锐角互余可得∠C=30![]() .
.
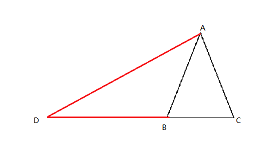
如图所示,若顶角∠BAC为锐角,则:
AB=BD,∠D=∠DAB
∵AB=AC∴∠ABC=∠C,
∴∠C=∠ABC=∠D+∠DAB=2∠D,
∵![]() ,
,
∴∠DAC=90![]() ,
,
∴∠C+∠D=3∠D=90![]() ,
,
∴∠D=30![]() ,
,
∴∠C=2∠D =60![]() ;
;

如图所示,若顶角∠BAC 为钝角,则:
AD=BD,∠B=∠DAB ,
∴∠ADC=∠B+∠DAB=2∠B,
∵AB=AC∴∠B=∠C,
∵![]() ,
,
∴∠DAC=90![]() ,
,
∴∠ADC+∠C=3∠C =90![]() ,
,
∴∠C =30![]() .
.
故答案为:30或60.

 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案【题目】如图棱长为a的小正方体,按照下图的方法继续摆放,自上而下分别叫第一层、第二层…第n层,第n层的小正方体的个数记为S.解答下列问题:
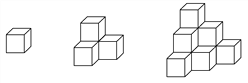
n | 1 | 2 | 3 | 4 | … |
S | 1 | 3 | … |
(1)按要求填写上表:
(2)研究上表可以发现S随n的变化而变化,且S随n的增大而增大有一定的规律,请你用式子来表示S与n的关系,并计算当n=10时,S的值为多少?
【题目】人民商场销售某种冰箱,每台进价为2500元,市场调研表明:当每台销售价定为2900元时,平均每天能售出8台;每台售价每降低50元,平均每天能多售出4台.
设该种冰箱每台的销售价降低了x元.
(1)填表:
每天售出的冰箱台数(台) | 每台冰箱的利润(元) | |
降价前 | 8 | |
降价后 |
(2)若商场要想使这种冰箱的销售利润平均每天达到5000元,则每台冰箱的售价应定为多少元?