题目内容
【题目】如图,在四边形ABCD中,∠B=∠C=90°,AB>CD,AD=AB+CD,∠ADC的平分线DE,交BC于点E.
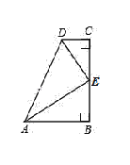
证明:①EC=EB;②AE⊥DE.
【答案】见解析
【解析】
(1)过点E作EF⊥AD于F,根据角平分线上的点到角的两边距离相等可得CE=EF,再求出BE=EF,从而得出结论.
(2)证AE是∠DAB的角平分线,即可求出答案.
证明:(1)如图,过点E作EF⊥AD于F,
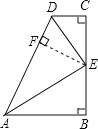
∵∠B=90°,DE平分∠CDA,
∴CE=EF,
又∵DE=DE,
∴RtDCE≌RtDFE.
∴DC=DF.
∵AD=AB+CD=DF+AF,
∴AB=AF.
又∵AE=AE,
∴RtAEB≌RtAFE.
∴EB=EF.
∴EB=CE.
(2)∵EB=CE,EF⊥AD,AB⊥BC,
∴AE平分∠BAD.
∵∠C=∠B=90°,
∴∠D+∠B=180°,
∴DC∥AB,
∴∠CDA+∠BAD=180°,
∵DE平分∠ADC,AE平分∠BAD,
∴∠EAD=![]() ∠BAD,∠EDA=
∠BAD,∠EDA=![]() ∠CDA,
∠CDA,
∴∠EAD+∠EDA=90°,
∴∠AED=180°﹣90°=90°.
∴AE⊥DE.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目