Question

【题目】如图,在平面直角坐标系中, ⊙O的半径是1,直线AB与x轴交于点P(x,0),且与x轴的正半轴夹角为45°,若直线AB与⊙O有公共点,则x值的范围是(　　)

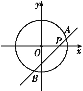
A. -1≤x≤1 B. -≤x≤ C. -<x< D. 0≤x≤

Answer 1

【答案】B

【解析】

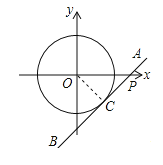
设直线AB的解析式为y=x+b，当直线与圆相切时切点为C，连接OC，则OC=1，由于直线AB与x轴正方向夹角为45°，所以△AOC是等腰直角三角形，故OC=PC=1再根据勾股定理求出OA的长即可．

∵直线AB与x轴正方向夹角为45°，
∴设直线AB的解析式为y=x+b，切点为C，连接OC，
∵⊙O的半径为1，
∴△AOC是等腰直角三角形，
∴OC=PC=1，
∴OA==，
∴P（，0），
同理可得，当直线与x轴负半轴相交时，P（，0），
∴-≤x≤．

故选：B