题目内容
 如图,在梯形ABCD中,AD∥BC,E为CD中点,连接AE并延长AE交BC的延长线于点F
如图,在梯形ABCD中,AD∥BC,E为CD中点,连接AE并延长AE交BC的延长线于点F
(1)求证:CF=AD;
(2)若AD=2,AB=8,当BC为多少时,点B在线段AF的垂直平分线上,为什么?
(1)证明:∵AD∥BC,
∴∠F=∠DAE.
又∵∠FEC=∠AED,
∴∠ECF=∠ADE,
∵E为CD中点,
∴CE=DE,
在△FEC与△AED中,
∵ ,
,
∴△FEC≌△AED.
∴CF=AD;
(2)解:当BC=6时,点B在线段AF的垂直平分线上,
其理由是:
∵BC=6,AD=2,AB=8,
∴AB=BC+AD.
又∵CF=AD,BC+CF=BF,
∴AB=BF.
∴△ABF是等腰三角形,
∴点B在AF的垂直平分线上.
分析:(1)通过求证△FEC≌△AED来证明CF=AD;
(2)若点B在线段AF的垂直平分线上,则应有AB=BF∵AB=8,CF=AD=2,∴BC=BF-CF=8-2=6时有AB=BF.
点评:本题利用了:(1)梯形的性质,(2)全等三角形的判定和性质,(3)中垂线的性质.
∴∠F=∠DAE.
又∵∠FEC=∠AED,
∴∠ECF=∠ADE,
∵E为CD中点,
∴CE=DE,
在△FEC与△AED中,
∵
 ,
,∴△FEC≌△AED.
∴CF=AD;
(2)解:当BC=6时,点B在线段AF的垂直平分线上,
其理由是:
∵BC=6,AD=2,AB=8,
∴AB=BC+AD.
又∵CF=AD,BC+CF=BF,
∴AB=BF.
∴△ABF是等腰三角形,
∴点B在AF的垂直平分线上.
分析:(1)通过求证△FEC≌△AED来证明CF=AD;
(2)若点B在线段AF的垂直平分线上,则应有AB=BF∵AB=8,CF=AD=2,∴BC=BF-CF=8-2=6时有AB=BF.
点评:本题利用了:(1)梯形的性质,(2)全等三角形的判定和性质,(3)中垂线的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
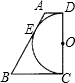 如图,在梯形ABCD中,AD∥BC,∠BCD=90°,以CD为直径的半圆O切AB于点E,这个梯形的面积为21cm2,周长为20cm,那么半圆O的半径为( )
如图,在梯形ABCD中,AD∥BC,∠BCD=90°,以CD为直径的半圆O切AB于点E,这个梯形的面积为21cm2,周长为20cm,那么半圆O的半径为( )| A、3cm | B、7cm | C、3cm或7cm | D、2cm |
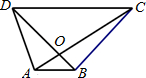 11、如图,在梯形ABCD中,AB∥CD,对角线AC、BD交于点O,则S△AOD
11、如图,在梯形ABCD中,AB∥CD,对角线AC、BD交于点O,则S△AOD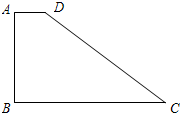 已知:如图,在梯形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=CD=10.
已知:如图,在梯形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=CD=10.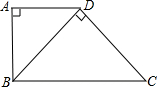 如图,在梯形ABCD中,AD∥BC,AB⊥AD,对角线BD⊥DC.
如图,在梯形ABCD中,AD∥BC,AB⊥AD,对角线BD⊥DC. 20、如图,在梯形ABCD中,AD∥BC,并且AB=8,AD=3,CD=6,并且∠B+∠C=90°,则梯形面积S梯形ABCD=
20、如图,在梯形ABCD中,AD∥BC,并且AB=8,AD=3,CD=6,并且∠B+∠C=90°,则梯形面积S梯形ABCD=