题目内容
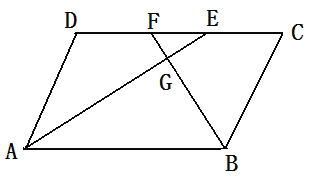
【题目】平行四边形ABCD中， AE、BF分别平分∠DAB和∠ABC交CD于点E、F.AE、BF交于点G.
(1)求证AE⊥BF
(2)判断DE和CF的大小关系，并说明理由.
【答案】（1）证明见解析；（2）DE=CF，理由见解析.
【解析】试题分析：（1）本题利用平行线的性质和角平分线的性质求出即可；（2）本题要先给出答案，证明利用角平分线和平行线的性质构造出等腰三角形.
试题解析：
(1)∵AE平分∠DAB BF平分∠ABC
∴∠BAE=∠DAB ∠ABF=∠ABC
∵AD∥BC ∴∠DAB+∠ABC=180°∴∠BAE+∠ABF=90°∴AE⊥CF
（2）DE=EF
∵AE平分∠DAB ∴∠DAE=∠EAB ∵DC∥AB∴∠EAB=∠DEA ∴∠DAE=∠DEA∴DE=AD
同理CF=BC 而 AD=BC ∴DE=CF
练习册系列答案
阅读快车系列答案
相关题目
