题目内容
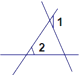
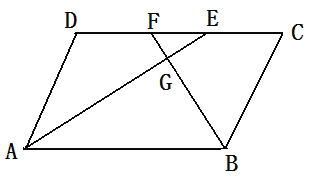
【题目】如图,点O是△ABC边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)求证:OE=OF;
(2)若CE=8,CF=6,求OC的长;

【答案】(1)证明见解析;(2)5.
【解析】试题分析:(1)根据平行线的性质以及角平分线的性质得出∠1=∠2,∠3=∠4,进而得出答案; (2)根据已知得出∠2+∠4=∠5+∠6=90°,进而利用勾股定理求出EF的长,即可得出CO的长.
试题解析:
(1)证明:∵MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,
∴∠2=∠5,4=∠6,
∵MN∥BC,
∴∠1=∠5,3=∠6,
∴∠1=∠2,∠3=∠4,
∴EO=CO,FO=CO,
∴OE=OF;
(2)∵∠2=∠5,∠4=∠6,
∴∠2+∠4=∠5+∠6=90°,
∵CE=8,CF=6,
∴EF=![]()
∴OC=EF=5;


练习册系列答案
相关题目
【题目】某中学图书馆将图书分为自然科学、文学艺术、社会百科、哲学四类.在“读书月”活动中,为了了解图书的借阅情况,图书管理员对本月各类图书的借阅进行了统计,表)和图是图书管理员通过采集数据后,绘制的两幅不完整的频率分布表与频数分布直方图.请你根据图表中提供的信息,解答以下问题:
各种图书 | 频数 | 频率 |
自然科学 | 400 | 0.20 |
文学艺术 | 1000 | 0.50 |
社会百科 | m | 0.25 |
哲学 | n |
(1)表中m= ,n= ;
(2)在图中,将表示“自然科学”的部分补充完整;
(3)若该学校打算采购一万册图书,请你估算“哲学”类图书应采购多少册较合适?
(4)根据图表提供的信息,请你提出一条合理化的建议.