题目内容
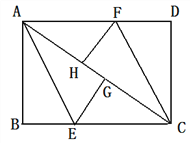
【题目】如图，在矩形ABCD中，AC是对角线，E、F分别在BC、AD边上，将边AB沿AE折叠，点B落在对角线AC上的G处，将边CD沿CF折叠，点D落在对角线AC上的点H处 .
(1)求证：四边形AECF是平行四边形.
(2)若AB=6，AC=10，求BE的长.
【答案】（1）证明见解析；（2）3.
【解析】试题分析：（1）利用三角形全等得出BE=DF,近而得出AF=CE，利用一组对边平行且相等得出平行四边形即可；（2）利用勾股定理得出BC的值，设BE=x，利用勾股定理在直角三角形ECG中求出x的值即可.
试题解析：
（1）易证ΔABE≌ΔAGE≌ΔCDF≌ΔCHF∴BE=DF ∵AD=BC∴AF=CE 又 AF∥CE∴四边形AECF是平行四边形
（2）∵AB=6 AC=10则BC=8 设BE=x∴EG=x EC=8-x∵AG=AB=6∴CG=4
∵EG2+GC2=EC2 ∴x2+42=(8-x)2 解得x=3∴BE=3
练习册系列答案
小学学习好帮手系列答案
小学同步三练核心密卷系列答案
相关题目
