题目内容
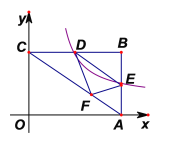
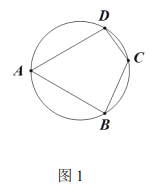
【题目】如图1,四边形![]() 内接于直径为
内接于直径为![]() 的圆,
的圆,![]() .
.
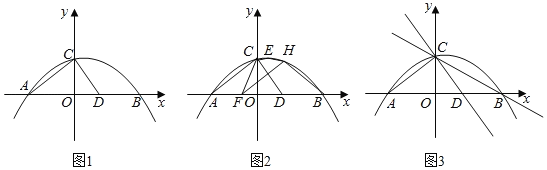
(1)①![]() _ ;
_ ;
②四边形![]() 的周长最大值为_ ;
的周长最大值为_ ;
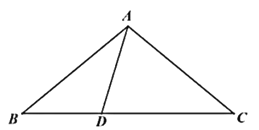
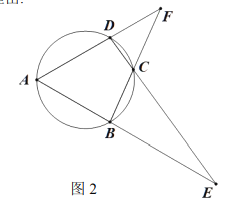
![]() 如图2,延长
如图2,延长![]() 相交于点
相交于点![]() ,延长
,延长![]() 相交于点
相交于点![]() 求
求![]() 与的
与的![]() 积;
积;
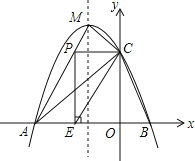
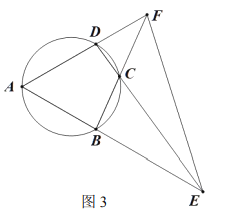
![]() 如图3,连接
如图3,连接![]() 请问在线段
请问在线段![]() 上是否存在点
上是否存在点![]() 与点
与点![]() 关于直线
关于直线![]() 对称,若存在,请证明;若不存在,请说明理由.
对称,若存在,请证明;若不存在,请说明理由.
【答案】(1)①![]() ;②
;②![]() ;(2)108;(3)存在,理由见解析
;(2)108;(3)存在,理由见解析
【解析】
(1)①连接BD,根据题意得出△ABD为等边三角形,再分别作△ABD三边的垂直平分线BE、DF、AM交于点O,则点O即为该圆的圆心,之后利用![]() 求出DM,由此进一步求解即可得出答案;②如图,延长BC到点E,使CE=CD,连接DE,再过点B作BF垂直于ED的延长线于点F,根据题意进一步证明△DCE为等边三角形,从而得出BC+CD=BC+CE=BE,然后进一步分析得出当
求出DM,由此进一步求解即可得出答案;②如图,延长BC到点E,使CE=CD,连接DE,再过点B作BF垂直于ED的延长线于点F,根据题意进一步证明△DCE为等边三角形,从而得出BC+CD=BC+CE=BE,然后进一步分析得出当![]() 时,BE最大,据此通过分析即可得出答案;
时,BE最大,据此通过分析即可得出答案;
(2)连接![]() ,根据题意首先证明∠1=∠F,∠2=∠E,从而得出
,根据题意首先证明∠1=∠F,∠2=∠E,从而得出![]() ,然后利用相似三角形性质得出
,然后利用相似三角形性质得出![]() ,据此即可求出
,据此即可求出![]() ;
;
(3)作点![]() 与点
与点![]() 关于直线
关于直线![]() 对称,并连接
对称,并连接![]() ,
,![]() ,结合(2)中的证明得出
,结合(2)中的证明得出![]() ,由此可得
,由此可得![]() ,即
,即![]() ,据此,根据题意再接着证明
,据此,根据题意再接着证明![]() ,从而即可得出
,从而即可得出![]() 、
、![]() 、
、![]() 在同一直线上,即在线段
在同一直线上,即在线段![]() 上存在点
上存在点![]() 与点
与点![]() 关于直线
关于直线![]() 对称.
对称.
(1)
①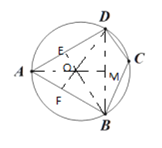
如图,连接BD,
∵AB=AD,∠A=60°,
∴△ABD为等边三角形,
再分别作△ABD三边的垂直平分线BE、DF、AM交于点O,则点O即为该圆的圆心,
∴AO=DO=BO=6,∠ODM=30°,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
②如图,延长BC到点E,使CE=CD,连接DE,再过点B作BF垂直于ED的延长线于点F,
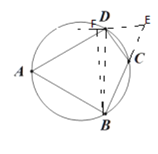
∵∠A=60°,
∴∠DCB=120°,
∴∠DCE=60°,
∵DC=CE,
∴△DCE为等边三角形,
∴∠E=60°,BC+CD=BC+CE=BE,
在Rt△BFE中,![]() ,
,
∵![]() ,
,
∴当![]() 时,BE最大,
时,BE最大,
∴此时![]() ,
,
∴四边形![]() 的周长最大值为:
的周长最大值为:![]() ,
,
故答案为:①![]() ;②
;②![]() ;
;
(2)如图,连接![]() ,
,
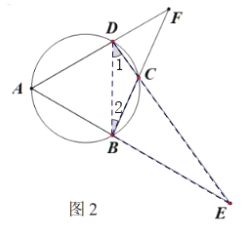
∵∠A=60°,AB=AD,四边形![]() 内接于圆,
内接于圆,
∴∠DCB=120°,∠ADB=∠ABD=60°,![]() ,
,
∴∠1+∠E=∠ABD=60°,![]() ,
,![]() ,
,
∴∠1=∠F,∠2=∠E,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
(3)存在,理由如下:
如图,作点![]() 与点
与点![]() 关于直线
关于直线![]() 对称,并连接
对称,并连接![]() ,
,![]() ,
,
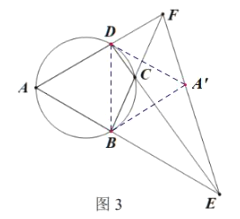
∵△ABD是等边三角形,点![]() 与点
与点![]() 关于直线
关于直线![]() 对称,
对称,
∴![]() 60°,
60°,![]() 60°,
60°,![]() ,
,
∴![]() 60°,
60°,
由(2)可知:![]()
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]()
∴![]() 、
、![]() 、
、![]() 在同一直线上,
在同一直线上,
∴在线段![]() 上存在点
上存在点![]() 与点
与点![]() 关于直线
关于直线![]() 对称.
对称.

 阅读快车系列答案
阅读快车系列答案