Question

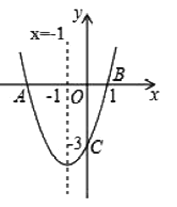
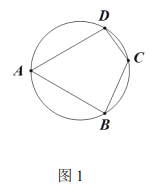
【题目】如图1，二次函数yx2x+3的图象交x轴于A、B两点(点A在点B的左侧)，交y轴于C点，连结AC，过点C作CD⊥AC交AB于点D．

（1）求点D的坐标；

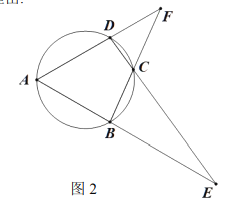
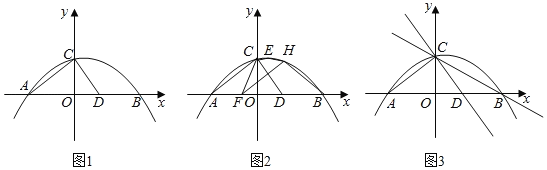
（2）如图2，已知点E是该二次函数图象的顶点，在线段AO上取一点F，过点F作FH⊥CD，交该二次函数的图象于点H(点H在点E的右侧)，当五边形FCEHB的面积最大时，求点H的横坐标；

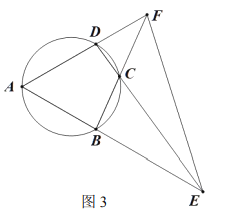
（3）如图3，在直线BC上取一点M(不与点B重合)，在直线CD的右上方是否存在这样的点N，使得以C、M、N为顶点的三角形与△BCD全等？若存在，请求出点N的坐标；若不存在，请说明理由．

Answer 1

【答案】（1）D(，0)；（2）H的横坐标为；（3）满足要标的N点坐标有：(，)、(3，3)、(，)．

【解析】

（1）先根据抛物线解析式求出A、B、C的坐标，由射影定理可得OD长度，从而求出D点坐标；

（2）设H点的横坐标为m，然后将五边形FCEHB的面积表示成关于m的二次函数，利用配方法可求得面积的最大值以及对应的H点坐标；

（3）由B、C、D的坐标可以求得DC、DB、BC的长度，然后分类讨论，分别画出符合要求的对应图形进行计算即可．

（1）令x=0，则y=3，∴C(0，3)，∴OC=3．

令y=0，则x2x+3=0，

解得：x1=﹣4，x2=6，

∴A(﹣4，0)，B(6，0)，∴OA=4，OB=6．

∵CD⊥AC，∴∠ACD=90°．

∵CO⊥AD，

∴OC2=OAOD，

∴OD，∴D(，0)．

（2）∵yx2x+3(x﹣1)2，

∴E(1，)．

如图2，连接OE、BE，作HG⊥x轴于点G，交BE于点P．

由B、E两点坐标可求得直线BE的解析式为：yx．

设H(m，m2m+3)，则P(m，m)，

∴HGm2m+3，HP=m2m，

∴S△BHE(xB﹣xE)HP(m2m)m2m．

∵FH⊥CD，AC⊥CD，∴AC∥FH，∴∠HFG=∠CAO．

∵∠AOC=∠FGH=90°，∴△ACO△FHG，

∴，∴FGHGm2m+4，

∴AF=AG﹣FG=m+4m2m﹣4m2m，

∴S△AFCAFOC(m2m)m2+m．

∵S四边形ACEB=S△ACO+S△OCE+S△OEB4×33×16，

∴S五边形FCEHB=S四边形ACEB+S△BHE﹣S△AFC(m2m)﹣(m2+m

m2m+15(m)2，

∴当m时，S五边形FCEHB取得最大值．

此时，H的横坐标为．

（3）∵B(6，0)，C(0，3)，D(，0)，

∴CD=BD，BC=3，

∴∠DCB=∠DBC．

①如图3﹣1，△CMN≌△DCB，MN交y轴于K，

则CM=CN=DC=DB，MN=BC=3，∠CMN=∠CNM=∠DBC=∠DCB，∴MN∥AB，∴MN⊥y轴，

∴∠CKN=∠COB=90°，MK=NKMN，

∴△CKN△COB，∴，

∴CK，∴OK=OC+CK，

∴N(，)．

②如图3﹣2，△MCN≌△DBC，

则CN=CB=3，∠MCN=∠DBC，

∴CN∥AB，∴N(3，3)．

③如图3﹣3，△CMN≌△DBC，

则∠CMN=∠DCB，CM=CN=DC=DB，MN=BC=3，

∴MN∥CD，

作MR⊥y轴于R，

则，

∴CR，RM，

∴OR=3，

作MQ∥y轴，NQ⊥MQ于点Q，

则∠NMQ=∠DCO，∠NQM=∠DOC=90°，

∴△COD△MQN，∴，

∴MQMN，NQMN，

∴NQ﹣RM，OR+MQ，

∴N(，)．

综上所述：满足要标的N点坐标有：

(，)、(3，3)、(，)．