题目内容
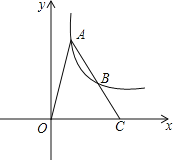
【题目】如图,在平面直角坐标系中,∠ACO=90°,∠AOC=30°,分别以AO、CO为边向外作等边三角形△AOD和等边三角形△COE,DF⊥AO于F,连DE交AO于G.
(1)求证:△DFG≌△EOG;
(2)H为AD的中点,连HG,求证:CD=2HG;
(3)在(2)的条件下,AC=4,若M为AC的中点,求MG的长.
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
(1)本题考查全等三角形的判定,通过等边三角形的性质利用AAS定理解答本题.
(2)本题考查三角形中位线定理以及全等三角形的判定,通过构造辅助线利用SAS定理解答.
(3)本题考查三角形中位线定理以及等边三角形的证明,通过构造辅助线,结合角度的计算加以证明,最后求解边长.
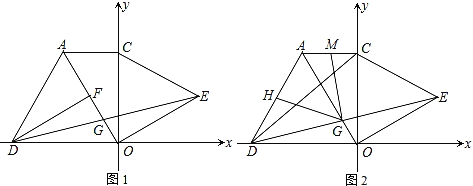
证明:(1)如图1,∵∠AOC=30°,
∴∠GOE=90°.
设AC=a,则OA=2a,OE=OC=![]() a,
a,
在等边△AOD中,DF⊥OA,
∴DF=![]() a,
a,
∴DF=OE.
又∵∠DGF=∠EGO,∠DFG=∠EOG,
∴△DFG≌△EOG(AAS).
(2)如下图图2所示,连接AE,
∵H、G分别为AD、DE的中点,
∴HG∥AE,HG=![]() AE.
AE.
∵DO=AO,CO=OE,∠DOC=∠AOE=90°,
∴△DOC≌△AOE(SAS),
∴DC=AE,
∴DC=2HG.
(3)如下图图2所示,连接HM,
∵H、M分别为AD、AC的中点,
∴HM=![]() CD.
CD.
∵DC=2HG,
∴HM=HG.
又∠DHG=∠DAE=60°+∠OAE=60°+∠ODC,∠AHM=∠ADC,
∴∠MHG=180°﹣∠AHM﹣∠DHG=180°﹣∠ADC﹣60°﹣∠ODC=120°﹣(∠ADC+∠ODC)=120°﹣∠ADO=60°,
∴△HMG为等边三角形.
∵AC=4,
∴OA=OD=8,OC=![]() ,CD=
,CD=![]() ,
,
∴MG=HG=![]() CD=
CD=![]() .
.

 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案