题目内容
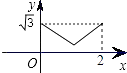
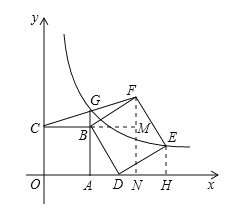
【题目】如图,在平面直角坐标系xOy中,四边形OABC是正方形,点A,C的坐标分别为(2,0),(0,2),D是x轴正半轴上的一点(点D在点A的右边),以BD为边向外作正方形BDEF(E,F两点在第一象限),连接FC交AB的延长线于点G.若反比例函数![]() 的图象经过点E,G两点,则k的值为 ______________.
的图象经过点E,G两点,则k的值为 ______________.

【答案】5
【解析】分析: 过F作FN垂直于x轴,交CB延长线于点M,利用AAS得到三角形ABD与三角形BMF全等, 利用全等三角形对应边相等得到AD=FM,进而表示出F坐标, 根据B为CM中点,得出G的CF中点,表示出G坐标,进而得出E坐标, 把G与E代入反比例解析式求出a的值,确定出E坐标,代入反比例解析式求出k的值即可.
详解: 过F作FN⊥x轴,交CB的延长线于点M,过E作EH⊥x轴,交x轴于点H,
∵∠FBM+∠MBD=90°,∠MBD+∠ABD=90°,
∴∠FBM=∠ABD,
∵四边形BDEF为正方形,
∴BF=BD,
在△ABD和△BMF中,
∠BAD=∠BMF,∠ABD=∠MFB,BD=BF,
∴△ABD≌△BMF(AAS),
设AD=FM=a,则有F(4,2+a),C(0,2),
由三角形中位线可得G为CF的中点,
∴G(2,2+12a),同理得到△DHE≌△BAD,
∴EH=AD=a,OH=OA+AD+DH=4+a,
∴E(4+a,a),∴2(2+12a)=a(4+a),即a2+3a-4=0,解得:a=1或a=-4(舍去),
∴E(5,1),
把F代入反比例解析式得:k=5.
故答案为:5.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目