题目内容
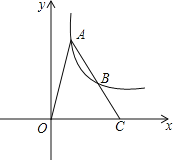
【题目】已知：直线
与x轴、y轴分别相交于点A和点B，点C在线段AO上.将
沿BC折叠后，点O恰好落在AB边上点D处．
（1）求出OC的长？
（2）点E、F是直线BC上的两点，若
是以EF为斜边的等腰直角三角形，求点F的坐标；
（3）取AB的中点M，若点P在y轴上，点Q在直线AB上，是否存在以C、M、P、Q为顶点的四边形为平行四边形？若存在，请求出所有满足条件的Q点坐标；若不存在，请说明理由．
【答案】（1）OC的长为3；（2）
或
；（3）
或
或
．
【解析】
（1）先根据一次函数的解析式可得点A、B坐标，从而可得OA、OB、AB的长，再根据折叠的性质可得
，然后在
中，利用勾股定理即可得；
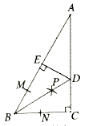
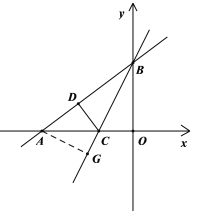
（2）如图，先由（1）得出点C坐标，再利用待定系数法可求出直线BC的函数解析式，从而可得出直线AG的函数解析式，然后联立直线BC、AG的函数解析式可求出点G的坐标，从而可得AG的长，最后根据等腰直角三角形的性质可得
，由此建立方程求解即可得；
（3）先求出点M坐标，再利用待定系数法可求出直线CM的函数解析式，设点Q的坐标为
，然后分MQ为所构成的平行四边形的边和MQ为所构成的平行四边形的对角线两种情况，分别根据平行四边形的性质、两点之间的距离公式列出等式求解即可．
（1）对于
当
时，
，解得
，则点A坐标为
当
时，
，则点B坐标为
由折叠的性质得：
，
设
，则
在中，
，即
解得
故OC的长为3；
（2）由（1）可得：点C坐标为
设直线BC的解析式为
将点，代入得：
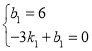，解得
则直线BC的解析式为
如图，过点A作直线BC的垂线，交直线BC于点G
则可设直线AG的解析式为
将点代入得：
，解得
则直线AG的解析式为
联立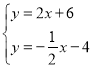
，解得
即点G坐标为
由两点之间的距离公式得：
点E、F是直线BC上的两点，且
是以EF为斜边的等腰直角三角形
设点F的坐标为
则有
整理得：
解得
或
当时，
当时，
则点F的坐标为或；
（3）由题意得：点M坐标为
，即
设直线CM的函数解析式为
将点、代入得：
，解得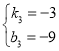
则直线CM的函数解析式为
因为点Q在直线AB：上
所以可设点Q的坐标为
由平行四边形的定义，分以下两种情况：
①MQ为所构成的平行四边形的边，则
设直线CP的函数解析式为
将点代入得：
，解得
则直线CP的函数解析式为
当时，
，则此时点P坐标为
由两点之间的距离公式得：
则
解得
或
当时，
当时，
因此，此时点Q的坐标为或
②MQ为所构成的平行四边形的对角线，则
设直线PQ的函数解析式为
将点代入得：
，解得
则直线PQ的函数解析式为
当时，
，则此时点P坐标为
由两点之间的距离公式得：
解得或
当时，
此时点Q的坐标为，点P的坐标为，则MQ不是所构成的平行四边形的对角线，不符题设，舍去
当时，
因此，此时点Q的坐标为
综上，所求的点Q的坐标为或或．
