题目内容
【题目】如图1,抛物线y=x2﹣2x+k与x轴交于A、B两点,与y轴交于点C(0,﹣3).[图2、图3为解答备用图]
(1)k= , 点A的坐标为 , 点B的坐标为;
(2)设抛物线y=x2﹣2x+k的顶点为M,求四边形ABMC的面积;
(3)在x轴下方的抛物线上是否存在一点D,使四边形ABDC的面积最大?若存在,请求出点D的坐标;若不存在,请说明理由;
(4)在抛物线y=x2﹣2x+k上求点Q,使△BCQ是以BC为直角边的直角三角形.
【答案】
(1)-3;(﹣1,0);(3,0)
(2)
解:∵y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴抛物线的顶点为M(1,﹣4),连接OM.
则△AOC的面积= ![]() ,△MOC的面积=
,△MOC的面积= ![]() ,
,
△MOB的面积=6,
∴四边形ABMC的面积=△AOC的面积+△MOC的面积+△MOB的面积=9.
说明:也可过点M作抛物线的对称轴,将四边形ABMC的面
积转化为求1个梯形与2个直角三角形面积的和
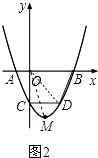
(3)
解:如图(2),设D(m,m2﹣2m﹣3),连接OD.
则0<m<3,m2﹣2m﹣3<0
且△AOC的面积= ![]() ,△DOC的面积=
,△DOC的面积= ![]() m,
m,
△DOB的面积=﹣ ![]() (m2﹣2m﹣3),
(m2﹣2m﹣3),
∴四边形ABDC的面积=△AOC的面积+△DOC的面积+△DOB的面积
=﹣ ![]() m2+
m2+ ![]() m+6
m+6
=﹣ ![]() (m﹣
(m﹣ ![]() )2+
)2+ ![]() .
.
∴存在点D( ![]() ,
, ![]() ),使四边形ABDC的面积最大为
),使四边形ABDC的面积最大为 ![]()
(4)
解:有两种情况:
如图(3),过点B作BQ1⊥BC,交抛物线于点Q1、交y轴于点E,连接Q1C.
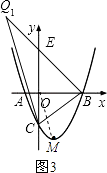
∵∠CBO=45°,
∴∠EBO=45°,BO=OE=3.
∴点E的坐标为(0,3).
∴直线BE的解析式为y=﹣x+3.
由 ![]()
解得 ![]()
∴点Q1的坐标为(﹣2,5).
如图(4),过点C作CF⊥CB,交抛物线于点Q2、交x轴于点F,连接BQ2.
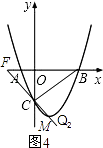
∵∠CBO=45°,
∴∠CFB=45°,OF=OC=3.
∴点F的坐标为(﹣3,0).
∴直线CF的解析式为y=﹣x﹣3.
由 ![]()
解得 ![]()
![]()
∴点Q2的坐标为(1,﹣4).
综上,在抛物线上存在点Q1(﹣2,5)、Q2(1,﹣4),使△BCQ1、△BCQ2是以BC为直角边的直角三角形.
说明:如图(4),点Q2即抛物线顶点M,直接证明△BCM为直角三角形同样可以.
【解析】解:(1)把C(0,﹣3)代入抛物线解析式y=x2﹣2x+k中得k=﹣3
∴y=x2﹣2x﹣3,
令y=0,
即x2﹣2x﹣3=0,
解得x1=﹣1,x2=3.
∴A(﹣1,0),B(3,0).
【考点精析】利用二次函数的图象和二次函数的性质对题目进行判断即可得到答案,需要熟知二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.

【题目】如图,正方形ABCD内部有若干个点,用这些点以及正方形ABCD的顶点A、B、C、D把原正方形分割成一些三角形(互相不重叠):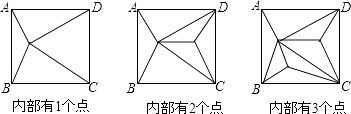
(1)填写如表:
正方形ABCD内点的个数 | 1 | 2 | 3 | 4 | … | n |
分割成的三角形的个数 | 4 | 6 | … |
(2)如果原正方形被分割成2016个三角形,此时正方形ABCD内部有多少个点?
(3)上述条件下,正方形又能否被分割成2017个三角形?若能,此时正方形ABCD内部有多少个点?若不能,请说明理由.
(4)综上结论,你有什么发现?(写出一条即可)




