题目内容
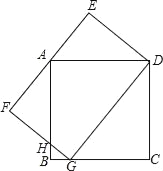
【题目】如图,G是边长为4的正方形ABCD的边BC上的一点,矩形DEFG的边EF过A,GD=5.
(1)指出图中所有的相似三角形;
(2)求FG的长.
【答案】(1)△AFH,△DCG,△DEA,△GBH均是相似三角形;(2)FG=![]() .
.
【解析】
(1)根据都是直角,其余两个角加起来为90°,根据对顶角、余角等关系,可以看出△AFH,△DCG,△DEA,△GBH均是相似三角形.
(2)根据![]() ,可以求出FG,由ED=FG,只要求出
,可以求出FG,由ED=FG,只要求出![]() =
=![]() 即可,因为△DEA∽△DCG,可以求出.
即可,因为△DEA∽△DCG,可以求出.
解:(1)△AFH,△DCG,△DEA,△GBH均是相似三角形;
(2)由∠E=∠C=90°,∠EDA与∠CDG均
为∠ADG的余角,得△DEA∽△DCG
∴![]() =
=![]() ,ED=FG,
,ED=FG,
∴![]() ,
,
由已知GD=5,AD=CD=4,
∴![]() ,即FG=
,即FG=![]() .
.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目