题目内容
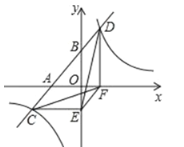
【题目】如图，抛物线y=ax2+bx(a＜0）过点E(10,0)，矩形ABCD的边AB在线段OE上（点A在点B的左边），点C，D在抛物线上．设A(t,0)，当t=2时，AD=4．
（1）求抛物线的函数表达式．
（2）当t为何值时，矩形ABCD的周长有最大值？最大值是多少？
（3）保持t=2时的矩形ABCD不动，向右平移抛物线．当平移后的抛物线与矩形的边有两个交点G，H，且直线GH平分矩形的面积时，求抛物线平移的距离．
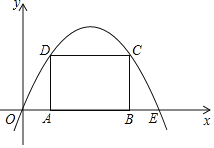
【答案】（1）
；（2）当t=1时，矩形ABCD的周长有最大值，最大值为
；（3）抛物线向右平移的距离是4个单位．
【解析】
（1）由点E的坐标设抛物线的交点式，再把点D的坐标（2，4）代入计算可得；
（2）由抛物线的对称性得BE=OA=t，据此知AB=10-2t，再由x=t时AD=
，根据矩形的周长公式列出函数解析式，配方成顶点式即可得；
（3）由t=2得出点A、B、C、D及对角线交点P的坐标，由直线GH平分矩形的面积知直线GH必过点P，根据AB∥CD知线段OD平移后得到的线段是GH，由线段OD的中点Q平移后的对应点是P知PQ是△OBD中位线，据此可得．
（1）设抛物线解析式为
，
当
时，
，
点
的坐标为
，
将点坐标代入解析式得
，
解得：
，
抛物线的函数表达式为
；
（2）由抛物线的对称性得
，
，
当
时，
，
矩形
的周长
，
，
，
，
当
时，矩形的周长有最大值，最大值为；
（3）如图，
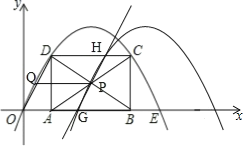
当时，点
、
、
、的坐标分别为
、
、
、，
矩形对角线的交点
的坐标为
，
直线
平分矩形的面积，
点是和
的中点，
，
由平移知，
是
的中位线，
，
所以抛物线向右平移的距离是4个单位．
练习册系列答案
天天练口算系列答案
相关题目
