题目内容
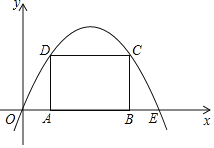
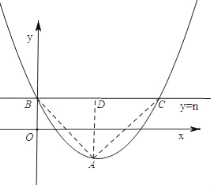
【题目】已知直线y＝n与二次函数y＝
（x﹣2）2﹣1的图象交于点B，点C，二次函数图象的顶点为A，当△ABC是等腰直角三角形时，则n的值为（ ）
A. 1B. 
C. 2﹣D. 2+
【答案】A
【解析】
设B（x1，n）、C（x2，n）．因为△ABC是等腰直角三角形，作AD⊥BC，所以AD＝
BC，即BC＝2AD，AD＝n﹣（﹣1）＝n+1，即：BC＝|x1-x2|＝
＝
＝
，所以
＝2（n+1），容易求出n＝1．
设B（x1，n）、C（x2，n），作AD⊥BC，垂足为D连接AB，AC，
∵y＝（x﹣2）2﹣1，
∴顶点A（2，﹣1），
AD＝n﹣（﹣1）＝n+1
∵直线y＝n与二次函数y＝（x﹣2）2﹣1的图象交于点B、C，
∴（x﹣2）2﹣1＝n，
化简，得x2﹣4x+2﹣2n＝0，
x1+x2＝4，x1x2＝2﹣2n，
∴BC＝|x1﹣x2|＝＝＝，
∵点B、C关于对称轴直线AD对称，
∴D为线段BC的中点，
∵△ABC是等腰直角三角形，
∴AD＝BC，
即BC＝2AD
＝2（n+1），
∴（2+2n）＝（n+1）2，
化简，得n2＝1，
∴n＝1或﹣1，
n＝﹣1时直线y＝n经过点A，不符合题意舍去，
所以n＝1．
故选：A．
练习册系列答案
相关题目
