题目内容
【题目】平面直角坐标系中有两点![]() 、
、![]() ,我们定义
,我们定义![]() 、
、![]() 两点间的“
两点间的“![]() 值”直角距离为
值”直角距离为![]() ,且满足
,且满足![]() ,其中
,其中![]() .小静和佳佳在解决问题:(求点
.小静和佳佳在解决问题:(求点![]() 与点
与点![]() 的“1值”直角距离
的“1值”直角距离![]() )时,采用了两种不同的方法:
)时,采用了两种不同的方法:
(方法一):![]() ;
;
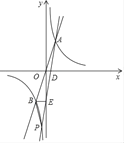
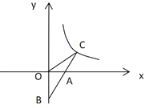
(方法二):如图1,过点![]() 作
作![]() 轴于点
轴于点![]() ,过点
,过点![]() 作直线
作直线![]() 与
与![]() 轴交于点
轴交于点![]() ,则
,则![]()
请你参照以上两种方法,解决下列问题:
(1)已知点![]() ,点
,点![]() ,则
,则![]() 、
、![]() 两点间的“2值”直角距离
两点间的“2值”直角距离![]() .
.
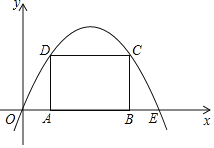
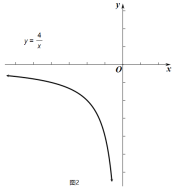
(2)函数![]() 的图像如图2所示,点
的图像如图2所示,点![]() 为其图像上一动点,满足
为其图像上一动点,满足![]() 两点间的“
两点间的“![]() 值”直角距离
值”直角距离![]() ,且符合条件的点
,且符合条件的点![]() 有且仅有一个,求出符合条件的“
有且仅有一个,求出符合条件的“![]() 值”和点
值”和点![]() 坐标.
坐标.
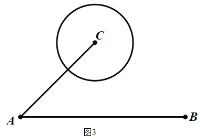
(3)城市的许多街道是相互垂直或平行的,因此,往往不能沿直线行走到达目的地,只能按直角拐弯的方式行走,因此,两地之间修建垂直和平行的街道常常转化为两点间的“![]() 值”直角距离,
值”直角距离,![]() 地位于
地位于![]() 地的正东方向上,
地的正东方向上,![]() 地在
地在![]() 点东北方向上且相距
点东北方向上且相距![]() ,以
,以![]() 为圆心修建了一个半径为
为圆心修建了一个半径为![]() 的圆形湿地公园,现在要在公园和
的圆形湿地公园,现在要在公园和![]() 地之间修建观光步道.步道只能东西或者南北走向,并且东西方向每千米成本是20万元,南北方向每千米的成本是10万元,问:修建这一规光步道至少要多少万元?
地之间修建观光步道.步道只能东西或者南北走向,并且东西方向每千米成本是20万元,南北方向每千米的成本是10万元,问:修建这一规光步道至少要多少万元?

【答案】(1)10 (2)![]() ,
,![]() (3)
(3)![]()
【解析】
(1)根据直角距离的公式,直接代入求解即可;
(2)设点C的坐标为![]() ,代入直角距离公式可得
,代入直角距离公式可得![]() 根据根的判别式求出k的值,即可求出点C的坐标;
根据根的判别式求出k的值,即可求出点C的坐标;
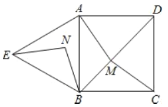
(3)如图,⊙C与线段AC交于点D,过点D作![]() 与AB交于点E,先证明△ADE是等腰直角三角形,从而得出
与AB交于点E,先证明△ADE是等腰直角三角形,从而得出![]() ,再根据直角距离的定义,即可求出出最低的成本.
,再根据直角距离的定义,即可求出出最低的成本.
(1)∵![]() ,点
,点![]() ,点
,点![]()
∴![]() ;
;
(2)设点C的坐标为![]()
∵![]()
∴![]()
∵![]()
∴![]()
∴![]()
∵符合条件的点![]() 有且仅有一个,且
有且仅有一个,且![]()
∴![]()
解得![]()
∴![]()
![]()
![]()
解得![]()
∴![]()
故![]() ,
,![]() ;
;
(3)如图,⊙C与线段AC交于点D,过点D作![]() 与AB交于点E
与AB交于点E
由题意得![]()
∴![]()
∵![]()
∴△ADE是等腰直角三角形
∴![]()
∵步道只能东西或者南北走向,并且东西方向每千米成本是20万元,南北方向每千米的成本是10万元
∴步道的最短距离为A和D的直角距离,即![]()
最低总成本![]() (万元)
(万元)
故修建这一规光步道至少要![]() 万元.
万元.

【题目】随着信息技术的快速发展,“互联网+”渗透到我们日常生活的各个领域,网上在线学习交流已不再是梦,现有某教学网站策划了A,B两种上网学习的月收费方式:
收费方式 | 月使用费/元 | 包时上网时间/h | 超时费/(元/min) |
A | 7 | 25 | 0.01 |
B | m | n | 0.01 |
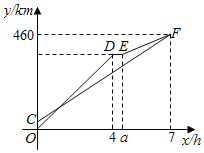
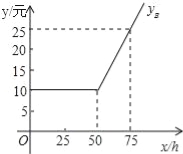
设每月上网学习时间为x小时,方案A,B的收费金额分别为yA,yB.
(1)如图是yB与x之间函数关系的图象,请根据图象填空:m= ;n=
(2)写出yA与x之间的函数关系式.
(3)选择哪种方式上网学习合算,为什么?
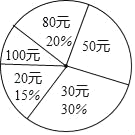
【题目】在“全民读书月”活动中,小明调查了班级里40名同学本学期购买课外书的费用情况,并将结果绘制成如图所示的统计表和扇形统计图,请根据相关信息,解答下列问题:(直接填写结果)
费用(元) | 20 | 30 | 50 | 80 | 100 |
人数 | 6 | a | 10 | b | 4 |
(1)本次调查获取的样本数据的众数是 元,中位数是 元;
(2)扇形统计图中,“50元”所对应的圆心角的度数为 度,该班学生购买课外书的平均费用为 元;
(3)若该校共有学生1000人,根据样本数据,估计本学期购买课外书花费50元的学生有 人.