��Ŀ����
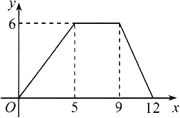
����Ŀ����֪������y=��![]() x2+
x2+![]() x+4��x���ڵ�A��B����y���ڵ�C������AC��BC��
x+4��x���ڵ�A��B����y���ڵ�C������AC��BC��
��1����A��B�������Լ�ֱ��BC�Ľ���ʽ��
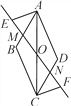
��2����ͼ1������P�ӵ�B������ÿ��5����λ���ٶ����O�˶�������P��y���ƽ���߽��߶�BC�ڵ�M�����������ڵ�N������N��NC��BC��BC�ڵ�K������MNK����MPB�������Ϊ1��2ʱ����P���˶�ʱ��t��ֵ��
��3����ͼ2������P �ӵ�B������ÿ��5����λ���ٶ����A�˶���ͬʱ��һ������Q�ӵ�A������AC����ͬ�ٶ����յ�C�˶�����P��Qͬʱֹͣ���ֱ���PQ��BPΪ����x���Ϸ���������PQEF��������BPGH�������ζ��㰴˳ʱ��˳����������PQEF��������BPGH�ص�������һ����Գ�ͼ��ʱ���������ʱ��Գ�ͼ�ε������

���𰸡���1��y=��x+4��2��PB=1��t=![]() ��3����
��3����![]() ��
��![]()
�������������������1����y=0���ⷽ����![]() x2+
x2+![]() x+4=0���������A��B���꣬�����ô���ϵ�������ֱ��BC��
x+4=0���������A��B���꣬�����ô���ϵ�������ֱ��BC��
��2����ͼ1�У���P��a��0����ֻҪ֤��MN=PB���г����̼��ɽ�����⣮
��3������ͼ2�У�����Գ�ͼ��Ϊ����ʱ���г���������˶�ʱ�伴�ɣ�����ͼ3�У�����Գ�ͼ����������ʱ���г��������ʱ�伴�ɣ�
�����������1����y=0������![]() x2+
x2+![]() x+4=0�����x=4����3��
x+4=0�����x=4����3��
����A���꣨��3��0������B���꣨4��0����
��ֱ��BC����ʽΪy=kx+b����B��4��0����C��0��4������
��![]() �����
�����![]() ��
��
��ֱ��BC����ʽΪy=��x+4��
��2����ͼ1�У���PN��OC��NK��BC��
���MPB=��MKN=90����
�ߡ�PMB=��NMK��
���MNK�ס�MPB��
�ߡ�MNK����MPB�������Ϊ1��2��
��BM=![]() MN��
MN��
��OB=OC��
���PBM=45����
��BM=P![]() B��
B��
��MN=PB����P��a��0������MN=��![]() a2+
a2+![]() a+4+a��4=��
a+4+a��4=��![]() a2+
a2+![]() a��BP=4��a��
a��BP=4��a��
����![]() a2+
a2+![]() a=4��a��
a=4��a��
���a=3��4����������
��PB=1��t=![]() ��
��

��3����ͼ2�У�����Գ�ͼ��Ϊ����ʱ��PF=PG��GM=FM��

��BP=PG=AQ��PQ=PF��
��AQ=PQ=5t��
����Q��QN��AP����AN=NP������AQN�ס�ACQ��
��![]() ��
��
��![]() ��
��
��AN=3t��
��AP=2AN=6t��
��AP+BP=AB��
��5t+6t=7��
��t=![]() ��
��
��PB=PF=![]() ��
��
����ACO�ס�FPR�ס�MFT��
��![]() ��
��
��FR=![]() ��TF=
��TF=![]() ��
��
��![]() ��
��
��FM=![]() ��
��
��S=2��![]() ��PF��FM=
��PF��FM=![]() ��
��
����ͼ3�У�����Գ�ͼ����������ʱ��
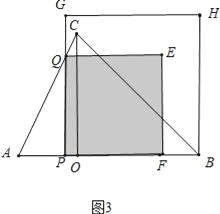
3t+5t=7��
��t=![]() ��
��
��S=![]() ��
��