��Ŀ����
����Ŀ���ڡ�ABC�У���A=90�㣬AB=4��AC=3��M��AB�ϵĶ��㣨����A��B�غϣ�����M����MN��BC��AC�ڵ�N��
��1����ͼ1���ѡ�AMN��ֱ��MN�۵��õ���PMN����AM=x��
i������P�����ڱ�BC�ϣ���x��ֵ��
ii����M���˶������У��ǡ�MNP������BCNM�غϵ����Ϊy������y����x�ĺ�����ϵʽ������y�����ֵ��
��2����ͼ2����MNΪֱ������O�����ڡ�O�����ڽӾ���AMQN�����ж�ֱ��BC���O��λ�ù�ϵ����˵�����ɣ�

���𰸡���1��i����x=2ʱ����Pǡ�����ڱ�BC�ϣ�ii�� y=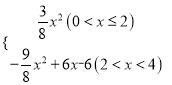 ����x=
����x=![]() ʱ���ص����ֵ���������ֵΪ2����2����x=
ʱ���ص����ֵ���������ֵΪ2����2����x=![]() ʱ����O��ֱ��BC���У���x��
ʱ����O��ֱ��BC���У���x��![]() ʱ����O��ֱ��BC���룻x��
ʱ����O��ֱ��BC���룻x��![]() ʱ����O��ֱ��BC�ཻ��
ʱ����O��ֱ��BC�ཻ��
�������������������1��i��������ԳƵ����ʣ��������ȵ��߶���ǣ��ɵõ�M��AB�е㣬����x=![]() AB=2ʱ����Pǡ�����ڱ�BC�ϣ�
AB=2ʱ����Pǡ�����ڱ�BC�ϣ�
ii��������������ۣ�����0��x��2ʱ����MNP������BCNM�غϵ����Ϊ��MNP�������������ԳƵ�������MNP�����������AMN���������y=![]() x2
x2
����2��x��4ʱ����ͼ2����PM��PN�ֱ�BC��E��F����i��֪ME=MB=4-x��PE=PM-ME=x-��4-x��=2x-4��������֪��PEF�ס�ABC���������������ε����ʼ�����ã�
��2�����÷������۵�˼�룬�����ֱ��BC����O����ʱ��x��ֵ��Ȼ��õ��ཻ������ʱx��ȡֵ��Χ��
�����������1��i����ͼ1��
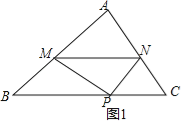
����Գ�����֪��AM=PM����AMN=��PMN��
��MN��BC��
���PMN=��BPM����AMN=��B��
���B=��BPM��
��AM=PM=BM��
����M��AB�е㣬����x=![]() AB=2ʱ����Pǡ�����ڱ�BC�ϣ�
AB=2ʱ����Pǡ�����ڱ�BC�ϣ�
ii�����·�����������ۣ�
����0��x��2ʱ��
��MN��BC��
���AMN�ס�ABC��
��![]() ��
��
��![]() ��
��
��AN= ![]() ��
��
��MNP������BCNM�غϵ����Ϊ��MNP�������
��![]() ��
��
����2��x��4ʱ����ͼ2��
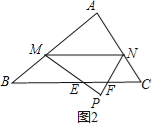
��PM��PN�ֱ�BC��E��F��
�ɣ�2��֪ME=MB=4-x��
��PE=PM-ME=x-��4-x��=2x-4��
������֪��PEF�ס�ABC��
��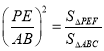 ��
��
��S��PEF=![]() ��x-2��2��
��x-2��2��
��y=S��PMN-S��PEF=![]() ��
��
����0��x��2ʱ��y=![]() x2��
x2��
����֪y���=![]() ��
��
������2��x��4ʱ��y=![]() ��
��
����x=![]() ʱ������2��x��4����y���=2��
ʱ������2��x��4����y���=2��
������������x=![]() ʱ���ص����ֵ���������ֵΪ2��
ʱ���ص����ֵ���������ֵΪ2��
��2������ͼ3��
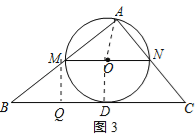
��ֱ��BC����O�����ڵ�D������AO��OD����AO=OD=![]() MN��
MN��
��Rt��ABC��BC=![]() =5��
=5��
�ɣ�1��֪��AMN�ס�ABC��
��![]() ����
����![]() ��
��
��MN=![]() x
x
��OD=![]() x��
x��
��M����MQ��BC��Q����MQ=OD=![]() x��
x��
��Rt��BMQ��Rt��BCA�У���B�ǹ����ǣ�
���BMQ�ס�BCA��
��![]() ��
��
��BM= ![]() ��AB=BM+MA=
��AB=BM+MA=![]() x+x=4
x+x=4
��x=![]() ��
��
����x=![]() ʱ����O��ֱ��BC���У�
ʱ����O��ֱ��BC���У�
��x��![]() ʱ����O��ֱ��BC���룻
ʱ����O��ֱ��BC���룻
x��![]() ʱ����O��ֱ��BC�ཻ��
ʱ����O��ֱ��BC�ཻ��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�