题目内容
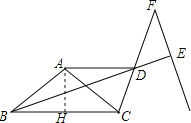
【题目】如本题图①,在△ABC中,已知∠ABC=∠ACB=α.过点A作BC的平行线与∠ABC的平分线交于点D,连接CD.
(1)求∠ACD的大小;
(2)在线段CD的延长线上取一点F,以FD为角的一边作∠DFE=α,另一边交BD延长线于点E,若FD=kAD(如本题图②所示),试求![]() 的值(用含k的代数式表示).
的值(用含k的代数式表示).

【答案】(1)∠ACD=90°﹣![]() ;(2)
;(2)![]() =
=![]() k2.
k2.
【解析】试题分析:(1)由∠ABC=∠ACB,BD平分∠ABC,得到∠1=∠2=![]() ,AB=AC,因为AD∥BC,推出∠2=∠3,得到∠3=∠1=
,AB=AC,因为AD∥BC,推出∠2=∠3,得到∠3=∠1=![]() ,得到AB=AD.AC=AD=AB.于是得到∠ACD=∠ADC=
,得到AB=AD.AC=AD=AB.于是得到∠ACD=∠ADC=![]() ,根据AD∥BC,∠CAD=ACB=α,得出结论∠ACD=∠ADC=
,根据AD∥BC,∠CAD=ACB=α,得出结论∠ACD=∠ADC=![]() =90°﹣
=90°﹣![]() .
.
(2)过A作AH⊥BC于点H,得到∠AHB=90°.证出∠BAH=90°﹣α,因为AD∥BC,得出∠BDC+∠ADC=180°,然后证得对应角相等,得到相似三角形,根据相似三角形的性质得比例式求得结果.
试题解析:(1)∵∠ABC=∠ACB,BD平分∠ABC,∴∠1=∠2=![]() ,AB=AC,
,AB=AC,
∵AD∥BC,∴∠2=∠3,∴∠3=∠1=![]() ,∴AB=AD.
,∴AB=AD.
∴AC=AD=AB.∴∠ACD=∠ADC=![]() ,
,
又∵AD∥BC,∴∠CAD=ACB=α,
∴∠ACD=∠ADC=![]() =90°﹣
=90°﹣![]() ;
;
(2)过A作AH⊥BC于点H,则∠AHB=90°.
∴∠BAH=90°﹣α,
∵AD∥BC,∴∠BDC+∠ADC=180°,即:∠BCA+∠ACD+∠CDB+∠3=180°,
由∠ACB=α,∠ACD=90°﹣![]() ,∠3=
,∠3=![]() ,
,
得:∠CDB=180°﹣α﹣(90°﹣![]() )﹣
)﹣![]() =90°﹣α.
=90°﹣α.
∴∠FDE=∠CDB=90°﹣α,∴∠BAH=∠FDE,∵∠ABH=∠DFE=α,
∴△ABH∽△DEF,
∵FD=kAD,AB=AD,∴S△DEF=k2S△BAH,
∵AD∥BC,∴S△BCD=S△ABC=2S△BAH,∴![]() =
=![]() k2,
k2,

 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案