题目内容
【题目】如图,O为ABCD的对角线AC的中点,过点O作一条直线分别与AB,CD交于点M,N,点E,F在直线MN上,且OE=OF.
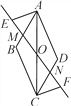
(1)图中共有几对全等三角形,请把它们都写出来;
(2)求证:∠MAE=∠NCF.
【答案】(1) 4对,△AMO≌△CNO,△OCF≌△OAE,△AME≌△CNF,△ABC≌△CDA;(2) 证明见解析
【解析】试题分析:(1)单个三角形全等的是:△AMO≌△CNO,△AME≌△CNF.由2部分组成全等的是:△OCF≌△OAE,△ABC≌△CDA;
(2)由题中已知条件可证得△OCF≌△OAE,进而求得∠EAO=∠FCO,而后利用平行四边形的对边平行的性质求得相应的内错角相等,进而求解.
试题解析:(1)有4对全等三角形.
分别为△AMO≌△CNO,△OCF≌△OAE,△AME≌△CNF,△ABC≌△CDA;
(2)∵OA=OC,∠1=∠2,OE=OF,
∴△OCF≌△OAE.
∴∠EAO=∠FCO.
在平行四边形ABCD中,AB∥CD,
∴∠BAO=∠DCO.
∴∠EAM=∠NCF.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目


