题目内容
【题目】如图,四边形ABCD内接于圆O ,AD、BC的延长线相交于点E,AB、DC的延长线相交于点F.
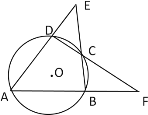
(1)若∠E=500, ∠F=400,求∠A的度数.
(2)探究∠E、∠F、∠A的关系并证明.
【答案】(1)45° ;(2)∠E+∠F+2∠A=180 °
【解析】
(1)根据圆内接四边形的对角互补,圆内接四边形的一个外角等于与它的内对角,和三角形外角的性质列式求解即可;
(2)根据圆内接四边形的对角互补,圆内接四边形的一个外角等于与它的内对角,和三角形外角的性质列式化简求解即可;
(1)∵∠CDE是△ADF的外角;
∴∠CDE=∠A+∠F,
∵∠F=40°,
∴∠CDE=∠A+40°,
∵∠CDE=∠ABE,
∴∠ABE=∠A+40°,
同理可证:∠ADF=∠A+∠E,
∵∠E=50°,
∴∠ADF=∠A+50°,
∵∠ABE+∠ADF=180°,
∴∠A+40°+∠A+50°=180°.
∴2∠A=180 °-90°=90°。
∴∠A=45°.
(2)∠E+∠F+2∠A=180 °理由如下:
∵∠CDE是△ADF的外角;
∴∠CDE=∠A+∠F,
∵∠CDE=∠ABE,
∴∠ABE=∠A+∠F,
同理可证:∠ADF=∠A+∠E,
∵∠ABE+∠ADF=180°,
∴∠A+∠F+∠A+∠E=180°.
∴∠E+∠F+2∠A=180 °

练习册系列答案
相关题目