Question

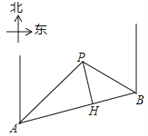
【题目】某条道路上通行车辆限速60千米/时，道路的AB段为监测区，监测点P到AB的距离PH为50米（如图）．已知点P在点A的北偏东45°方向上，且在点B的北偏西60°方向上，点B在点A的北偏东75°方向上，那么车辆通过AB段的时间在多少秒以内，可认定为超速？（参考数据：≈1.7，≈1.4）．

Answer 1

【答案】车辆通过AB段的时间在8.1秒以内，可认定为超速

【解析】分析：根据点到直线的距离的性质，构造直角三角形，然后利用解直角三角形的应用，解直角三角形即可.

详解：如图，由题意知∠CAB=75°，∠CAP=45°，∠PBD=60°，

∴∠PAH=∠CAB–∠CAP=30°，

∵∠PHA=∠PHB=90°，PH=50，∴AH===50，

∵AC∥BD，∴∠ABD=180°–∠CAB=105°，∴∠PBH=∠ABD–∠PBD=45°，

则PH=BH=50，∴AB=AH+BH=50+50，

∵60千米/时=米/秒，∴时间t==3+3≈8.1（秒），

即车辆通过AB段的时间在8.1秒以内，可认定为超速．