题目内容
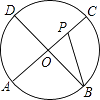
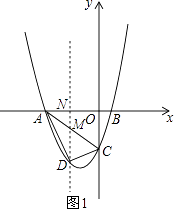
【题目】已知，如图，抛物线y=ax2+2ax+c（a＞0）与y轴交于点C，与x轴交于A，B两点，点A在点B左侧．点B的坐标为（1，0），OC=3OB．
（1）求抛物线的解析式；
（2）若点D是线段AC下方抛物线上的动点，求四边形ABCD面积的最大值；
（3）若点E在x轴上，点P在抛物线上．是否存在以A，C，E，P为顶点且以AC为一边的平行四边形？若存在，直接写出点P的坐标；若不存在，请说明理由．
【答案】
（1）
解：∵OC=3OB，B（1，0），
∴C（0，﹣3）．
把点B，C的坐标代入y=ax2+2ax+c，得a=1，c=﹣3，
∴抛物线的解析式y=x2+2x﹣3
（2）
解：由A（﹣3，0），C（0，﹣3）得直线AC的解析式为y=﹣x﹣3，
如图1，过点D作DM∥y轴分别交线段AC和x轴于点M，N．
设M（m，﹣m﹣3）则D（m，m2+2m﹣3），
DM=﹣m﹣3﹣（m2+2m﹣3）=﹣m2﹣3m=﹣（m+ 
）2+ 
，
∴﹣1＜0，
∴当x=- 时，DM有最大值 ，
∴S四边形ABCD=S△ABC+S△ACD= 
×4×3+ ×3×DM，此时四边形ABCD面积有最大值为6+ × = 
（3）
解：存在．
讨论：①如图2，过点C作CP1∥x轴交抛物线于点P1，过点P1作P1E1∥AC交x轴于点E1，
此时四边形ACP1E1为平行四边形．
∵C（0，﹣3），令﹣3=x2+2x﹣3
∴x1=0，x2=﹣2．
∴P1（﹣2，﹣3）．
②平移直线AC交x轴于点E，交x轴上方的抛物线于点P，当AC=PE时，四边形ACEP为平行四边形，
∵C（0，﹣3），
∴可令P（x，3），3=x2+2x﹣3，得x2+2x﹣6=0
解得x1=﹣1+ 
，x2=﹣1﹣ ，
此时存在点P2（﹣1+ ，3），P3（﹣1﹣ ，3），
综上所述，存在3个点符合题意，坐标分别是：
P1（﹣2，﹣3），P2（﹣1+ ，3），P3（﹣1﹣ ，3）．
【解析】（1）根据OC=3OB，B（1，0），求出C点坐标（0，﹣3），把点B，C的坐标代入y=ax2+2ax+c，求出a点坐标即可求出函数解析式；（2）图，过点D作DM∥y轴分别交线段AC和x轴于点M，N．设M（m，﹣m﹣3）则D（m，m2+2m﹣3），然后求出DM的表达式，把S四边形ABCD分解为S△ABC+S△ACD ， 转化为二次函数求最值；（3）①过点C作CP1∥x轴交抛物线于点P1 ， 过点P1作P1E1∥AC交x轴于点E1 ， 此时四边形ACP1E1为平行四边形．平移直线AC交x轴于点E，交x轴上方的抛物线于点P，当AC=PE时，四边形ACEP为平行四边形．
【题目】为了了解2012年全国中学生创新能力大赛中竞赛项目“知识产权”笔试情况，随机抽查了部分参赛同学的成绩，整理并制作图表如下：
分数段 | 频数 | 频率 |
60≤x＜70 | 30 | 0.1 |
70≤x＜80 | 90 | n |
80≤x＜90 | m | 0.4 |
90≤x≤100 | 60 | 0.2 |
请根据以上图表中提供的信息，解答下列问题：
（1）本次调查的样本容量为；
（2）在表中：m= ， n=；
（3）补全频数分布直方图；
（4）参加比赛的小聪说，他的比赛成绩是所有抽查同学成绩的中位数，据此推断他的成绩落在分数段内；
（5）如果比赛成绩80分以上（含80分）为优秀，那么你估计该竞赛项目的优秀率大约是 ．
