题目内容
【题目】有一座抛物线形拱桥，校下面在正常水位时AB宽20米，水位上升3米就达到警戒线CD，这时水面宽度为10米． 
（1）在如图的坐标系中，求抛物线的表达式；
（2）若洪水到来是水位以0.2米/时的速度上升，从正常水位开始，再过几小时能到达桥面？
【答案】
（1）解：设所求抛物线的解析式为y=ax2．
设D（5，b），则B（10，b﹣3），
把D、B的坐标分别代入y=ax2得： 
，解得 
，
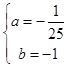∴抛物线的解析式为y=﹣ 
x2
（2）解：∵b=﹣1，∴拱桥顶O到CD的距离为1，
∴（1+3）÷0.2=20（小时），
所以再过20小时到达拱桥顶
【解析】（1）设所求抛物线的解析式为y=ax2 ． 把D（5，b），则B（10，b﹣3）代入解方程组即可．（2）根据时间=路程÷速度计算即可．
练习册系列答案
阅读快车系列答案
相关题目
