Question

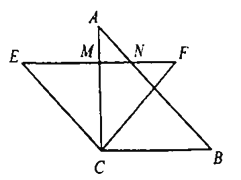
【题目】如图，在Rt△ABC中，∠C＝90°，∠B＝54°，AD是△ABC的角平分线．求作AB的垂直平分线MN交AD于点E，连接BE；并证明DE＝DB．（要求：尺规作图，保留作图痕迹，不写作法）

Answer 1

【答案】见解析．

【解析】

如图,利用基本作图作MN垂直平分AB得到点E,先计算出∠BAC=36°,再利用AD是△ABC的角平分线得到∠DAB=18°,再利用线段垂直平分线的性质和等腰三角形的性质得到∠EBA=∠EAB=18°,接着利用三角形外角性质得到∠DEB=36,然后计算出∠DBE=36°得到∠DEB=∠DBE,从而得到DE=DB

如图，点E为所作；

∵∠C＝90°，∠B＝54°，

∴∠BAC＝36°，

∵AD是△ABC的角平分线，

∴∠DAB＝ ×36°＝18°，

∵MN垂直平分AB，

∴EA＝EB，

∴∠EBA＝∠EAB＝18°，

∴∠DEB＝∠EAB+∠EBA＝36°，

∵∠DBE＝54°﹣18°＝36°，

∴∠DEB＝∠DBE，

∴DE＝DB．