Question

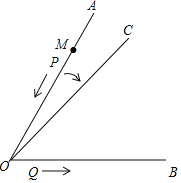
【题目】如图，已知∠AOB=60°，∠AOB的边OA上有一动点P，从距离O点18cm的点M处出发，沿线段MO、射线OB运动，速度为2cm/s；动点Q从点O出发，沿射线OB运动，速度为lcm/s；P、Q同时出发，同时射线OC绕着点O从OA上以每秒5°的速度顺时针旋转，设运动时间是t（s）．

（1）当点P在MO上运动时，PO=______cm（用含t的代数式表示）；

（2）当点P在线段MO上运动时，t为何值时，OP=OQ？此时射线OC是∠AOB的角平分线吗？如果是请说明理由．

（3）在射线OB上是否存在P、Q相距2cm？若存在，请求出t的值并求出此时∠BOC的度数；若不存在，请说明理由．

Answer 1

【答案】（1）（18-2t）；（2）详见解析；（3）t=16，∠BOC=20°或t=20，∠BOC=40°．

【解析】

（1）先确定出PM=2t，即可得出结论；

（2）先根据OP=OQ建立方程求出t=6，进而求出∠AOC=30°，即可得出结论；

（3）分P、Q相遇前相距2cm和相遇后2cm两种情况，建立方程求解，接口得出结论．

解：（1）当点P在MO上运动时，由运动知，PM=2t，

∵OM=18cm，

∴PO=OM-PM=（18-2t）cm，

故答案为：（18-2t）；

（2）由（1）知，OP=18-2t，

当OP=OQ时，则有18-2t=t，

∴t=6

即t=6时，能使OP=OQ，

∵射线OC绕着点O从OA上以每秒5°的速度顺时针旋转，

∴∠AOC=5°×6=30°，

∵∠AOB=60°，

∴∠BOC=∠AOB-∠AOC=30°=∠AOC，

∴射线OC是∠AOB的角平分线，

（3）分为两种情形．

当P、Q相遇前相距2cm时，

OQ-OP=2

∴t-（2t-18）=2

解这个方程，得t=16，

∴∠AOC=5°×16=80°

∴∠BOC=80°-60°=20°，

当P、Q相遇后相距2cm时，OP-OQ=2

∴（2t-18）-t=2

解这个方程，得t=20，

∴∠AOC=5°×20=100°

∴∠BOC=100°-60°=40°，

综合上述t=16，∠BOC=20°或t=20，∠BOC=40°．