题目内容
【题目】如图,矩形的边OA在x轴上,边OC在y轴上,点B的坐标为(10,8),沿直线OD折叠矩形,使点A正好落在BC上的E处,E点坐标为(6,8),抛物线y=ax2+bx+c经过O、A、E三点.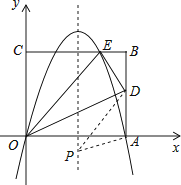
(1)求此抛物线的解析式;
(2)求AD的长;
(3)点P是抛物线对称轴上的一动点,当△PAD的周长最小时,求点P的坐标.
【答案】
(1)
解:∵四边形ABCD是矩形,B(10,8),
∴A(10,0),
又抛物线经过A、E、O三点,把点的坐标代入抛物线解析式可得
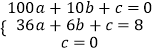 ,解得
,解得 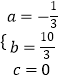 ,
,
∴抛物线的解析式为y=﹣ ![]() x2+
x2+ ![]() x
x
(2)
解:由题意可知:AD=DE,BE=10﹣6=4,AB=8,
设AD=x,则ED=x,BD=AB﹣AD=8﹣x,
在Rt△BDE中,由勾股定理可知ED2=EB2+BD2,即x2=42+(8﹣x)2,解得x=5,
∴AD=5;
(3)
解:∵y=﹣ ![]() x2+
x2+ ![]() x,
x,
∴其对称轴为x=5,
∵A、O两点关于对称轴对称,
∴PA=PO,
当P、O、D三点在一条直线上时,PA+PD=PO+PD=OD,此时△PAD的周长最小,
如图,连接OD交对称轴于点P,则该点即为满足条件的点P,
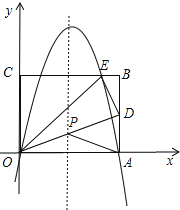
由(2)可知D点的坐标为(10,5),
设直线OD解析式为y=kx,把D点坐标代入可得5=10k,解得k= ![]() ,
,
∴直线OD解析式为y= ![]() x,
x,
令x=5,可得y= ![]() ,
,
∴P点坐标为(5, ![]() )
)
【解析】(1)利用矩形的性质和B点的坐标可求出A点的坐标,再利用待定系数法可求得抛物线的解析式;(2)设AD=x,利用折叠的性质可知DE=AD,在Rt△BDE中,利用勾股定理可得到关于x的方程,可求得AD的长;(3)由于O、A两点关于对称轴对称,所以连接OD,与对称轴的交点即为满足条件的点P,利用待定系数法可求得直线OD的解析式,再由抛物线解析式可求得对称轴方程,从而可求得P点坐标.本题主要考查二次函数的综合应用,涉及知识点有待定系数法、矩形的性质、勾股定理、轴对称的性质及方程思想.在(2)中注意方程思想的应用,在(3)中确定出满足条件的P点的位置是解题的关键.本题考查知识点虽然较多,但题目属于基础性的题目,难度不大.
【考点精析】关于本题考查的勾股定理的概念和矩形的性质,需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;矩形的四个角都是直角,矩形的对角线相等才能得出正确答案.

 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案