题目内容
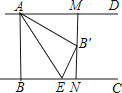
【题目】如图,在Rt△ABC中,∠ABC=90°,点M是AC的中点,以AB为直径作⊙O分别交AC,BM于点D,E.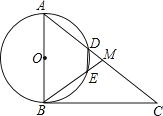
(1)求证:MD=ME;
(2)填空:
①若AB=6,当AD=2DM时,DE=;
②连接OD,OE,当∠A的度数为时,四边形ODME是菱形.
【答案】
(1)
证明:∵∠ABC=90°,AM=MC,
∴BM=AM=MC,
∴∠A=∠ABM,
∵四边形ABED是圆内接四边形,
∴∠ADE+∠ABE=180°,
又∠ADE+∠MDE=180°,
∴∠MDE=∠MBA,
同理证明:∠MED=∠A,
∴∠MDE=∠MED,
∴MD=ME
(2)2;60°
【解析】①由(1)可知,∠A=∠MDE,
∴DE∥AB,
∴ ![]() ,
,
∵AD=2DM,
∴DM:MA=1:3,
∴DE= ![]() AB=
AB= ![]() ×6=2.
×6=2.
故答案为2.
②当∠A=60°时,四边形ODME是菱形.
理由:连接OD、OE,
∵OA=OD,∠A=60°,
∴△AOD是等边三角形,
∴∠AOD=60°,
∵DE∥AB,
∴∠ODE=∠AOD=60°,∠MDE=∠MED=∠A=60°,
∴△ODE,△DEM都是等边三角形,
∴OD=OE=EM=DM,
∴四边形OEMD是菱形.
故答案为60°.
(1)先证明∠A=∠ABM,再证明∠MDE=∠MBA,∠MED=∠A即可解决问题.
(2)①由DE∥AB,得 ![]() =
= ![]() 即可解决问题.
即可解决问题.
②当∠A=60°时,四边形ODME是菱形,只要证明△ODE,△DEM都是等边三角形即可.本题考查圆内接四边形性质、直角三角形斜边中线性质、菱形的判定等知识,解题的关键是灵活运用这些知识解决问题,记住菱形的三种判定方法,属于中考常考题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目