题目内容
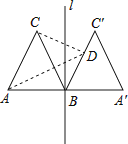
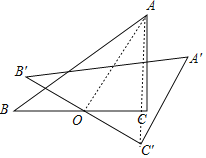
【题目】如图，在△ABC中，∠C=90°，AC=3，BC=4，点O是BC中点，将△ABC绕点O旋转得△A′B' C′，则在旋转过程中点A、C′两点间的最大距离是_______.
【答案】2+
【解析】
连接OA，AC′，如图，易得OC=2，再利用勾股定理计算出OA=，接着利用旋转的性质得OC′=OC=2，根据三角形三边的关系得到AC′≤OA+OC′（当且仅当点A、O、C′共线时，取等号），从而得到AC′的最大值．
解：连接OA，AC′，如图，
∵点O是BC中点，
∴OC=
BC=2，
在Rt△AOC中，OA=
,
∵△ABC绕点O旋转得△A′B'C′，
∴OC′=OC=2，
∵AC′≤OA+OC′（当且仅当点A、O、C′共线时，取等号），
∴AC′的最大值为2+，
即在旋转过程中点A、C′两点间的最大距离是2+ ．
故答案为2+．
练习册系列答案
相关题目
