题目内容

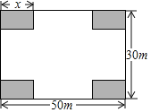
【题目】某社区决定把一块长50m，宽30m的矩形空地建成居民健身广场，设计方案如图，阴影区域为绿化区（四块绿化区为大小、形状都相同的矩形），空白区域为活动区，且四周的4个出口宽度相同，当绿化区较长边x为何值时，活动区的面积达到1341m2？

【答案】（5+）m

【解析】

先用x表示出绿化区的宽，再利用活动区的面积=空地面积-绿化区面积列一元二次方程，解方程求出x的值即可.

根据题意，绿化区的宽为：[30﹣（50﹣2x）]÷2＝x﹣10

∴50×30﹣4x（x﹣10）＝1341

﹣4x2+40x+1500＝1341，

4x2﹣40x﹣159＝0

x＝5±

∵5﹣＜0，(不符合题意，舍去)

∴x＝5+.

答：当绿化区较长边x为（5+）m时，活动区的面积达到1341m2.

练习册系列答案
相关题目

【题目】如图，AB是⊙O的直径，弦DE垂直平分半径OA，C为垂足，弦DF与半径OB相交于点P，连接EF、EO，若DE＝2，∠DPA＝45°．

（1）求⊙O的半径；

（2）求图中阴影部分的面积．

【题目】某中学开展了“手机伴我健康行”主题活动。他们随即抽取部分学生进行“使用手机的目的”和“每周使用手机的时间”的问卷调查，并绘制成如图①，②的统计图，已知“查资料”的人数是40人。

请你根据以上信息解答下列问题：

(1) 在扇形统计图中，“玩游戏”对应的百分比为___，圆心角度数是___度；

(2)补全条形统计图；

(3)该校共有学生2100人,估计每周使用手机时间在2小时以上(不含2小时)的人数

【题目】二次函数y＝a（x﹣h）2+k（a≠0）的图象是抛物线，定义一种变换，先作这条抛物线关于原点对称的抛物线y′，再将得到的对称抛物线y′向上平移m（m＞0）个单位，得到新的抛物线ym，我们称ym叫做二次函数y＝a（x﹣h）2+k（a≠0）的m阶变换．

（1）已知：二次函数y＝2（x+2）2+1，它的顶点关于原点的对称点为　 　，这个抛物线的2阶变换的表达式为　 　．

（2）若二次函数M的6阶变换的关系式为y6′＝（x﹣1）2+5．

①二次函数M的函数表达式为　 　．

②若二次函数M的顶点为点A，与x轴相交的两个交点中左侧交点为点B，在抛物线y6′＝（x﹣1）2+5上是否存在点P，使点P与直线AB的距离最短，若存在，求出此时点P的坐标．

（3）抛物线y＝﹣3x2﹣6x+1的顶点为点A，与y轴交于点B，该抛物线的m阶变换的顶点为点C．若△ABC是以AB为腰的等腰三角形,请直按写出m的值．

【题目】如图，已知二次函数y＝x2+bx+c的图象与x轴交于点A（1，0）、B（3，0），与y轴交于点C．

（1）求二次函数的解析式；

（2）若点P为抛物线上的一点，点F为对称轴上的一点，且以点A、B、P、F为顶点的四边形为平行四边形，求点P的坐标；

（3）点E是二次函数第四象限图象上一点，过点E作x轴的垂线，交直线BC于点D，求四边形AEBD面积的最大值及此时点E的坐标．

【题目】如图，△ABC中，AC=BC＜AB.若∠1、∠2分别为∠ABC、∠ACB的外角，则下列角度关系何者正确（ ）

A.

B.

C.

D.

【题目】在一个不透明的盒子中装有4张卡片.4张卡片的正面分别标有数字1,2,3,4,这些卡片除数字外都相同,将卡片搅匀.

(1)从盒子任意抽取一张卡片,恰好抽到标有奇数卡片的概率是： ；

(2)先从盒子中任意抽取一张卡片,再从余下的3张卡片中任意抽取一张卡片,求抽取的2张卡片标有数字之和大于4的概率(请用画树状图或列表等方法求解).

【题目】如图，有两条公路OM，ON相交成30°，沿公路OM方向离两条公路的交叉处O点80米的A处有一所希望小学，当拖拉机沿ON方向行驶时，距拖拉机中心50米的范围内均会受到噪音影响，已知有两台相距40米的拖拉机正沿ON方向行驶，它们的速度均为10米/秒，则这两台拖拉机沿ON方向行驶时给小学带来噪音影响的时间为 （ ）

A. 6秒B. 8秒C. 10秒D. 18秒

【题目】下列说法不正确的是（　　）

A.已知线段AB＝40cm，点P是线段AB的黄金分割点，且AP＞BP，则AP的长约为24.72cm

B.各有一个角是100°的等腰三角形相似

C.所有的矩形都相似

D.菱形既是轴对称图形，又是中心对称图形

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网