题目内容
【题目】如图,已知二次函数y=x2+bx+c的图象与x轴交于点A(1,0)、B(3,0),与y轴交于点C.

(1)求二次函数的解析式;
(2)若点P为抛物线上的一点,点F为对称轴上的一点,且以点A、B、P、F为顶点的四边形为平行四边形,求点P的坐标;
(3)点E是二次函数第四象限图象上一点,过点E作x轴的垂线,交直线BC于点D,求四边形AEBD面积的最大值及此时点E的坐标.
【答案】(1)y=x2﹣4x+3;(2)点P(4,3)或(0,3)或(2,﹣1);(3)最大值为![]() ,E(
,E(![]() ,﹣
,﹣![]() ).
).
【解析】
(1)用交点式函数表达式,即可求解;
(2)分当AB为平行四边形一条边、对角线,两种情况,分别求解即可;
(3)利用S四边形AEBD=![]() AB(yD﹣yE),即可求解.
AB(yD﹣yE),即可求解.
解:(1)用交点式函数表达式得:y=(x﹣1)(x﹣3)=x2﹣4x+3;
故二次函数表达式为:y=x2﹣4x+3;
(2)①当AB为平行四边形一条边时,如图1,
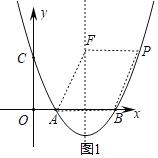
则AB=PE=2,
则点P坐标为(4,3),
当点P在对称轴左侧时,即点C的位置,点A、B、P、F为顶点的四边形为平行四边形,
故:点P(4,3)或(0,3);
②当AB是四边形的对角线时,如图2,
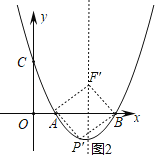
AB中点坐标为(2,0)
设点P的横坐标为m,点F的横坐标为2,其中点坐标为:![]() ,
,
即:![]() =2,解得:m=2,
=2,解得:m=2,
故点P(2,﹣1);
故:点P(4,3)或(0,3)或(2,﹣1);
(3)直线BC的表达式为:y=﹣x+3,
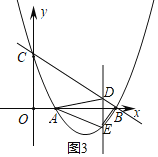
设点E坐标为(x,x2﹣4x+3),则点D(x,﹣x+3),
S四边形AEBD=![]() AB(yD﹣yE)=﹣x+3﹣x2+4x﹣3=﹣x2+3x,
AB(yD﹣yE)=﹣x+3﹣x2+4x﹣3=﹣x2+3x,
∵﹣1<0,故四边形AEBD面积有最大值,
当x=![]() ,其最大值为
,其最大值为![]() ,此时点E(
,此时点E(![]() ,﹣
,﹣![]() ).
).

练习册系列答案
相关题目