题目内容
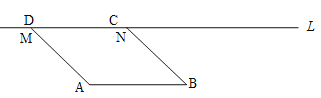
【题目】如图，有两条公路OM，ON相交成30°，沿公路OM方向离两条公路的交叉处O点80米的A处有一所希望小学，当拖拉机沿ON方向行驶时，距拖拉机中心50米的范围内均会受到噪音影响，已知有两台相距40米的拖拉机正沿ON方向行驶，它们的速度均为10米/秒，则这两台拖拉机沿ON方向行驶时给小学带来噪音影响的时间为 （ ）
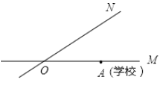
A. 6秒B. 8秒C. 10秒D. 18秒
【答案】C
【解析】
过点A作AC⊥ON，求出AC的长，第一台拖拉机到B点时开始对学校有噪音影响，然后可求出BC的长，第一台拖拉机到D点时噪音消失，此时第二台拖拉机已经产生噪音影响且与第一台拖拉机相距40米，故第二台拖拉机还须前行40米后才对学校没有噪音影响，依此计算即可.
解：如图，
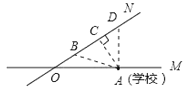
过点A作AC⊥ON，
∵∠MON＝30°，OA＝80米，
∴AC＝40米，
当第一台拖拉机到B点时对学校产生噪音影响，此时AB＝50米，
由勾股定理得：BC＝30米，
第一台拖拉机到D点时噪音消失，
所以CD＝30米，BD=60米，
由于两台拖拉机相距40米，则第一台拖拉机到D点时第二台已经产生噪音影响，且还须前行40米后才对学校没有噪音影响．
所以影响时间应是：(60+40)÷10＝10秒，
故选：C.
练习册系列答案
阳光试卷单元测试卷系列答案
相关题目
