题目内容
【题目】如图 ,![]() 是一元二次方程
是一元二次方程![]() 的两个实数根,且
的两个实数根,且![]() ,抛物线
,抛物线![]() 的图象经过
的图象经过![]() .
.

(1)求抛物线的解析式;
(2)设抛物线与![]() 轴的另一个交的为
轴的另一个交的为![]() ,抛物线的顶点为
,抛物线的顶点为![]() ,求
,求![]() 的面积.
的面积.
【答案】(1)![]() (2)3
(2)3
【解析】
(1)求出方程的两个实数根,即可得出点A,B的坐标,代入抛物线解析式得出b,c的值即可;
(2)根据抛物线解析式可求出点C、D的坐标,设抛物线的对称轴l与直线BC相交于点M,求出直线BC的解析式,进而得出M的坐标,从而得出三角形的面积.
解:(1)由![]() 解得
解得![]() ,
,![]()
∵![]() ∴
∴![]() ,
,![]() ∴
∴![]() ,
,![]()
则![]() ,解之得
,解之得![]()
因此该抛物线的解析式为![]()
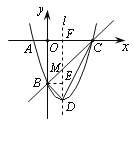
(2)抛物线![]() 的与x轴交点C的坐标为
的与x轴交点C的坐标为
(3,0),顶点D的坐标为(1,-4),抛物线的对称轴l与直线BC相交于点M,
设直线BC的解析式为![]() ,则
,则![]() ,解得
,解得![]()
∴直线BC的解析式为![]() ,
,
∴直线BC与对称轴l的交点M的坐标为(1,-2),∴ MD=2,
∴![]()
∴△BCD的面积为3.

 名题训练系列答案
名题训练系列答案 期末集结号系列答案
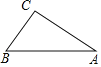
期末集结号系列答案【题目】祥云桥位于省城太原南部,该桥塔主体由三根曲线塔柱组合而成,全桥共设13对直线型斜拉索,造型新颖,是“三晋大地”的一种象征.某数学“综合与实践”小组的同学把“测量斜拉索顶端到桥面的距离”作为一项课题活动,他们制订了测量方案,并利用课余时间借助该桥斜拉索完成了实地测量.测量结果如下表.
项目 | 内容 | ||
课题 | 测量斜拉索顶端到桥面的距离 | ||
测量示意图 |
| 说明:两侧最长斜拉索AC,BC相交于点C,分别与桥面交于A,B两点,且点A,B,C在同一竖直平面内. | |
测量数据 | ∠A的度数 | ∠B的度数 | AB的长度 |
38° | 28° | 234米 | |
… | … | ||
(1)请帮助该小组根据上表中的测量数据,求斜拉索顶端点C到AB的距离(参考数据:sin38°≈0.6,cos38°≈0.8,tan38°≈0.8,sin28°≈0.5,cos28°≈0.9,tan28°≈0.5)
(2)该小组要写出一份完整的课题活动报告,除上表的项目外,你认为还需要补充哪些项目(写出一个即可).