题目内容
【题目】在△ABC中,AB=5,AC=8,BC=7,点D是BC上一动点,DE⊥AB于E,DF⊥AC于F,线段EF的最小值为_____.

【答案】![]()
【解析】
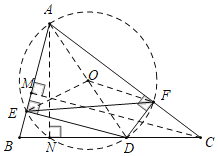
如图,作CM⊥AB于M,AN⊥BC于N.连接AD,OE,OF.设AM=x,则BM=5﹣x.根据![]() ,可得
,可得![]() ,解得x=4,推出∠EAF=60°,由A,E,D,F四点共圆,推出当⊙O的直径最小时,EF的长最小,根据垂线段最短可知:当AD与AN重合时,AD的值最小,由此即可解决问题.
,解得x=4,推出∠EAF=60°,由A,E,D,F四点共圆,推出当⊙O的直径最小时,EF的长最小,根据垂线段最短可知:当AD与AN重合时,AD的值最小,由此即可解决问题.
解:如图,作CM⊥AB于M,AN⊥BC于N.连接AD,OE,OF.设AM=x,则BM=5﹣x.
∵CM2=AC2﹣AM2=BC2﹣BM2,
∴82﹣x2=72﹣(5﹣x)2,
解得x=4,
∴AM=4,AC=2AM,
∴∠ACM=30°,∠CAM=60°,CM=![]() AM=4
AM=4![]() ,
,
∵S△ABC=![]() BCAN=
BCAN=![]() ABCM,
ABCM,
∴AN=![]() ,
,
∵DE⊥AB,DF⊥AC,
∴∠AED=∠AFD=90°,
∴A,E,D,F四点共圆,
∴当⊙O的直径最小时,EF的长最小,
根据垂线段最短可知:当AD与AN重合时,AD的值最小,AD的最小值为![]() ,
,
此时OE=OF=![]() ,EF=2OEcos30°=
,EF=2OEcos30°=![]() ,
,
∴EF的最小值为![]() ,
,
故答案为![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目