题目内容
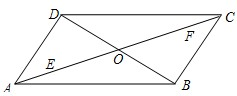 26、如图,已知平行四边形ABCD的对角线AC、BD相交于点O,AC=20cm、BD=12cm,两动点E、F同时分别以2cm/s的速度从点A、C出发在线段AC相对上运动.
26、如图,已知平行四边形ABCD的对角线AC、BD相交于点O,AC=20cm、BD=12cm,两动点E、F同时分别以2cm/s的速度从点A、C出发在线段AC相对上运动.(1)求证:当E、F运动过程中不与点O重合时,四边形BEDF一定为平行四边形;
(2)当E、F运动时间t为何值时,四边形BEDF为矩形?
分析:(1)连接DE,EB,BF,FD,根据已知可得AE=CF,根据对角线互相平分的四边形是平行四边形,可证明四边形BEDF为平行四边形;
(2)应考虑两种情况:当点E在OA上,点F在OC上时EF=BD=12cm,四边形BEDF为矩形;当点E在OC上,点F在OA上时,EF=BD=12cm,四边形BEDF为矩形.
(2)应考虑两种情况:当点E在OA上,点F在OC上时EF=BD=12cm,四边形BEDF为矩形;当点E在OC上,点F在OA上时,EF=BD=12cm,四边形BEDF为矩形.
解答: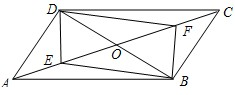 (1)解:连接DE,EB,BF,FD
(1)解:连接DE,EB,BF,FD
∵两动点E、F同时分别以2cm/s的速度从点A、C出发在线段AC相对上运动.
∴AE=CF
∵平行四边形ABCD的对角线AC、BD相交于点O,
∴OD=OB,OA=OC(平行四边形的对角线互相平分)
∴OA-AE=OC-CF或AE-OA=CF-OC
即OE=OF
∴四边形BEDF为平行四边形.(对角线互相平分的四边形是平行四边形)(4分)
(2)当点E在OA上,点F在OC上时EF=BD=12cm,
四边形BEDF为矩形
∵运动时间为t
∴AE=CF=2t
∴EF=20-4t=12
∴t=2(s)
当点E在OC上,点F在OA上时,EF=BD=12cm
EF=4t-20=12
∴t=8(s)
因此当E、F运动时间2s或8s时,四边形BEDF为矩形.(10分)
说明:如果学生有不同的解题方法.只要正确,可参照本评分标准,酌情给分.
 (1)解:连接DE,EB,BF,FD
(1)解:连接DE,EB,BF,FD∵两动点E、F同时分别以2cm/s的速度从点A、C出发在线段AC相对上运动.
∴AE=CF
∵平行四边形ABCD的对角线AC、BD相交于点O,
∴OD=OB,OA=OC(平行四边形的对角线互相平分)
∴OA-AE=OC-CF或AE-OA=CF-OC
即OE=OF
∴四边形BEDF为平行四边形.(对角线互相平分的四边形是平行四边形)(4分)
(2)当点E在OA上,点F在OC上时EF=BD=12cm,
四边形BEDF为矩形
∵运动时间为t
∴AE=CF=2t
∴EF=20-4t=12
∴t=2(s)
当点E在OC上,点F在OA上时,EF=BD=12cm
EF=4t-20=12
∴t=8(s)
因此当E、F运动时间2s或8s时,四边形BEDF为矩形.(10分)
说明:如果学生有不同的解题方法.只要正确,可参照本评分标准,酌情给分.
点评:此题主要考查平行四边形、矩形的判定.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
 CD的边长a等于点P,Q间的距离.
CD的边长a等于点P,Q间的距离. 如图,已知平行四边形ABCD的对角线AC,BD相交于点O,BD绕点O顺时针旋转交AB,DC于E,F.
如图,已知平行四边形ABCD的对角线AC,BD相交于点O,BD绕点O顺时针旋转交AB,DC于E,F.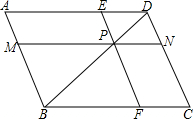 交AB、CD、AD、BC于M、N、E、F,设a=PM•PE,b=PN•PF.
交AB、CD、AD、BC于M、N、E、F,设a=PM•PE,b=PN•PF. 23、如图,已知平行四边形ABCD.
23、如图,已知平行四边形ABCD. 如图,已知平行四边形ABCD,作DE⊥AB,垂足为E,把三角形AED沿AB方向平移AB长个单位长度.
如图,已知平行四边形ABCD,作DE⊥AB,垂足为E,把三角形AED沿AB方向平移AB长个单位长度.