Question

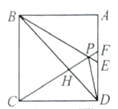
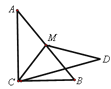
【题目】如图，在Rt△ABC中，∠ACB=90°，∠A＜∠B，沿△ABC的中线CM将△CMA折叠，使点A落在点D处，若CD恰好与MB垂直，则tanA的值为__________________．

Answer 1

【答案】

【解析】

根据折叠的性质，可得：∠D=∠A，∠MCD=∠MCA，再由直角三角形斜边中线的性质可得出∠MCD=∠D，从而确定∠A的度数，即可确定答案.

解：如图：

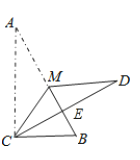
∵CM是直角AABC的中线

∴СМ=АМ=МВ=АВ，

∴∠A=∠ACM，

由折叠的性质可得：∠D=∠A，∠MCD=∠MCA，AM=DM，

∴MC=MD，∠A=∠ACM=∠MCD，

又∵AB⊥CD

∴∠CMB=∠DMB，∠CEB=∠MED=90°

∵∠B+∠A=90°，∠B+∠ECB=90°

∴∠A=∠ECB

∴∠A=∠ACM=∠MCE=∠ECB

∴∠A=∠ACB=30°

∴tanA=