题目内容
【题目】小琴的父母承包了一块荒山地种植一批梨树,今年收获一批金溪密梨,小琴的父母打算以m元/斤的零售价销售5000斤密梨;剩余的5000(m+1)斤密犁以比零售价低1元的批发价批给外地客商,预计总共可赚得55 000元的毛利润.

(1)求小琴的父母今年共收获金溪密梨多少斤?
(2)若零售金溪密梨平均每天可售出200斤,每斤盈利2元.为了加快销售和获得较好的售价,采取了降价措施,发现销售单价每降低0.1元,平均每天可多售出40斤,应降价多少元?每天销售利润为600元.
【答案】(1)小琴的父母今年共收获金溪密犁25000斤;(2)应降价0.5元,每天销售利润为600元.
【解析】
(1)根据秒利润的组成可得到方程,解出m,再求出金溪密梨的总斤数;
(2)设降了x个0.1元,根据题意可列出一元二次方程,即可求解.
(1)解:根据题意得:
5000m+5000(m+1)(m-1)=55000
解得:m1=3,m2=-4(不符合题意,舍去)
当m=3时,小琴的父母今年共收获金溪密犁为
5000+5000(m+1)=25000斤
小琴的父母今年共收获金溪密犁25000斤
(2)设降了x个0.1元,根据题意得
(200+40x)(2-0.1x)=600
解得:x1=5,x2=10
当x=5时,售价为2- 0.1x=1.5元
当x2=10时,售价为2- 0.1x=1元
∵为了加快销售和获得较好的售价
∴x=5
∴应降价0.5元,每天销售利润为600元

 阅读快车系列答案
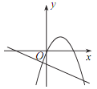
阅读快车系列答案【题目】2018年非洲猪瘟疫情暴发后,专家预测,2019年我市猪肉售价将逐月上涨,每千克猪肉的售价y1(元)与月份x(1≤x≤12,且x为整数)之间满足一次函数关系,如下表所示.每千克猪肉的成本y2(元)与月份x(1≤x≤12,且x为整数)之间满足二次函数关系,且3月份每千克猪肉的成本全年最低,为9元,如图所示.
月份x | … | 3 | 4 | 5 | 6 | … |
售价y1/元 | … | 12 | 14 | 16 | 18 | … |

(1)求y1与x之间的函数关系式.
(2)求y2与x之间的函数关系式.
(3)设销售每千克猪肉所获得的利润为w(元),求w与x之间的函数关系式,哪个月份销售每千克猪肉所第获得的利润最大?最大利润是多少元?