题目内容
【题目】如图，ABCD是一张边长为4cm的正方形纸片，E，F分别为AB，CD的中点，沿过点D的折痕将A角翻折，使得点A落在EF上的点A′处折痕交AE于点G，则∠ADG=____°EG=___cm ．
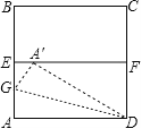
【答案】15
【解析】
由ABCD是一张边长为4cm的正方形纸片，E，F分别为AB，CD的中点，可得AE=DF=2cm，EF=AD=4cm，由翻折可得AG=A′G，AD=A′D，在Rt△DF
中，利用勾股定理可求得答案．求得
，在Rt△DF中利用正切值即可求得
度数，进而求得∠ADG度数；在Rt△EG中，设EG=x，则G=AG=2x，利用勾股定理即可求得x值．
∵ABCD是一张边长为4cm的正方形纸片，E、F分别为AB，CD的中点，
∴AE=DF=2cm，EF=AD=4cm，
DG为折痕，
∴AG=G，AD=D，
Rt△DF中，
∴
∴∠ADG＝∠DG＝
∴
Rt△EG中，设EG=x，则G=AG=2x，
∴x=
解得x=
故答案为：15°，
练习册系列答案
相关题目
【题目】为了迎接“十一”小长假的购物高峰．某运动品牌专卖店准备购进甲、乙两种运动鞋．其中甲、乙两种运动鞋的进价和售价如下表：
运动鞋 | 甲 | 乙 |
进价（元/双） | m | m﹣20 |
售价（元/双） | 240 | 160 |
已知：用3000元购进甲种运动鞋的数量与用2400元购进乙种运动鞋的数量相同．
（1）求m的值；
（2）要使购进的甲、乙两种运动鞋共200双的总利润（利润=售价﹣进价）不少于21700元，且不超过22300元，问该专卖店有几种进货方案？
（3）在（2）的条件下，专卖店准备对甲种运动鞋进行优惠促销活动，决定对甲种运动鞋每双优惠a（50＜a＜70）元出售，乙种运动鞋价格不变．那么该专卖店要获得最大利润应如何进货？
