题目内容
【题目】实践与探究:已知AB∥CD,点P是平面内一点.
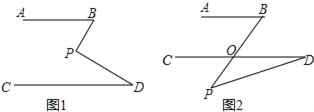
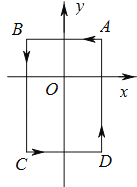
(1)如图1,若点P在AB、CD内部,请探究∠BPD、∠B、∠D之间有何数量关系?请证明你的结论.
(2)如图2,若点P移动到AB、CD外部,那么∠BPD、∠B、∠D之间的数量关系是否发生变化?请给出你的证明.
【答案】(1)∠BPD=∠B+∠D,证明见解析;(2)发生变化,应该为∠BPD=∠B﹣∠D,证明见解析.
【解析】
试题(1)作PQ∥AB,根据平行线的性质即可得∠BPD=∠B+∠D;
(2)作PE∥CD,根据平行线的性质即可得∠BPD=∠B-∠D;
试题解析:(1)∠BPD=∠B+∠D,证明如下:
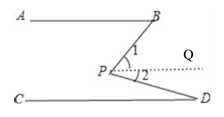
作PQ∥AB,如图,
∵AB∥CD,∴AB∥PQ∥CD,∴∠1=∠B,∠2=∠D,∴∠BPD=∠B+∠D .
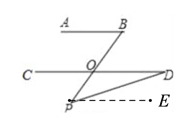
(2)发生变化,应该为∠BPD=∠B﹣∠D,证明如下:
过P做PE∥CD,∵AB∥CD,PE∥CD,∴ AB∥CE ,∴∠B=∠EPB, ∠D=∠EPD,而∠B=∠BPD+∠DPE,
∴∠B=∠BPD+∠D,即∠BPD=∠B﹣∠D.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
【题目】某射击队为从甲、乙两名运动员中选拔一人参加全国比赛,对他们进行了8次测试,测试成绩(单位:环)如下表:
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 | 第八次 | |
甲 | 10 | 8 | 9 | 8 | 10 | 9 | 10 | 8 |
乙 | 10 | 7 | 10 | 10 | 9 | 8 | 8 | 10 |
(1)根据表格中的数据,计算出甲的平均成绩是 环,乙的平均成绩是 环;
(2)分别计算甲、乙两名运动员8次测试成绩的方差;
(3)根据(1)(2)计算的结果,你认为推荐谁参加全国比赛更合适,并说明理由.