题目内容
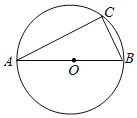
【题目】如图,在⊙O中,直径AB=10,tanA=![]() .
.
(1)求弦AC的长;
(2)D是AB延长线上一点,且AB=kBD,连接CD,若CD与⊙O相切,求k的值;
(3)若动点P以3cm/s的速度从A点出发,沿AB方向运动,同时动点Q以![]() cm/s的速度从B点出发沿BC方向运动,设运动时间为t (0<t<
cm/s的速度从B点出发沿BC方向运动,设运动时间为t (0<t<![]() ),连结PQ.当t为何值时,△BPQ为Rt△?
),连结PQ.当t为何值时,△BPQ为Rt△?
【答案】(1)5![]() ;(2)2;(3)
;(2)2;(3)![]() 秒或
秒或![]() 秒
秒
【解析】
(1)先利用特殊角的三角函数求出∠A,进而求出AC;
(2)先求出∠BOC=60°,进而得出∠D=30°,进而求出OD,即可求出BD,即可得出结论;
(3)先判断出点P在线段AB上,点Q在线段BC上,再分∠BQP=90°或∠BPQ=90°,最后用三角函数建立方程求解即可得出结论.
解:(1)∵⊙O的直径AB=10,
∴∠ACB=90°,
在Rt△ABC中,tanA=![]() ,
,
∴∠A=30°,
∴AC=ABcosA=10cos30°=10×![]() =5
=5![]() ,
,
即弦AC的长为5![]() ;
;
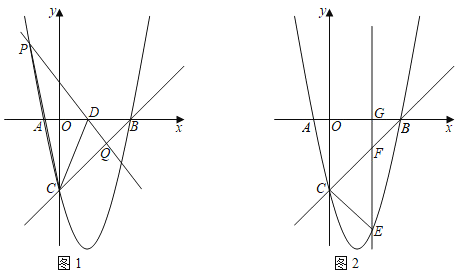
(2)如图1,连接OC,
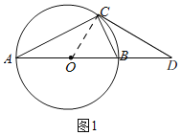
由(1)知,∠A=30°,
∴∠BOC=2∠A=60°,
∵CD是⊙O的切线,
∴∠OCD=90°,
∴∠D=90°﹣60°=30°,
∵OB=OC=![]() AB=5,
AB=5,
∴OD=2OC=10,
∴BD=OD﹣OB=10﹣5=5,
∵AB=kBD,
∴k=![]() =
=![]() =2,
=2,
即k的值为2;
(3)在Rt△ABC中,∵AB=10,∠A=30°,
∴BC=![]() AB=5,
AB=5,
由运动知,AP=3t,BQ=![]() ,
,
∵0<t<![]() ,
,
∴0<AP<10,0<BQ<5,
∴点P在线段AB上,点Q在线段BC上,
∵△BPQ为直角三角形,且∠ABC=90°﹣∠A=60°,
∴∠BQP=90°或∠BPQ=90°,
①当∠BQP=90°时,如图2,
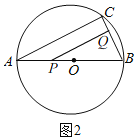
在Rt△BQP中,BP=AB﹣AP=10﹣3t,BQ=![]() t,∠ABC=60°,
t,∠ABC=60°,
∴cos∠ABC=![]() =
=![]() =
=![]() ,
,
∴t=![]() ,
,
②当∠BPQ=90°时,如图3,
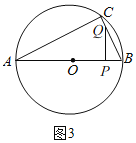
在Rt△BPQ中,cos∠ABC=![]() =
=![]() =
=![]() ,
,
∴t=![]() ,
,
即当t为![]() 秒或
秒或![]() 秒时,△BPQ为Rt△.
秒时,△BPQ为Rt△.

 名校课堂系列答案
名校课堂系列答案【题目】我市某社区今年准备新建一养老中心,其中规划建造三类养老专用房间共100间,这三类养老专用房间分别为单人间(1个养老床位),双人间(2个养老床位),三人间(3个养老床位),因实际需要,单人间房间数在10至30之间(包括10和30),且双人间的房间数是单人间的2倍,设规划建造单人间的房间数为![]() .
.
(1)根据题意,填写下表:
单人间的房间数 | 10 | … |
| … | 30 |
双人间的房间数 | _________ | … |
| … | 60 |
三人间的房间数 | 70 | … | _________ | … | _________ |
养老床位数 | 260 | … | _________ | … | _________ |
(2)若该养老中心建成后可提供养老床位200个,求![]() 的值;
的值;
(3)求该养老中心建成后最多提供养老床位多少个?最少提供养老床位多少个?