题目内容
【题目】某次篮球联赛初赛阶段,每队有![]() 场比赛,每场比赛都要分出胜负,每队胜一场得
场比赛,每场比赛都要分出胜负,每队胜一场得![]() 分, 负一场得
分, 负一场得![]() 分,积分超过
分,积分超过![]() 分才能获得参赛资格.
分才能获得参赛资格.
(1)已知甲队在初赛阶段的积分为![]() 分,求甲队初赛阶段胜、负各多少场;
分,求甲队初赛阶段胜、负各多少场;
(2)如果乙队要获得参加决赛资格,那么乙队在初赛阶段至少要胜多少场?
【答案】91) 甲队胜了8场,则负了2场;(2) 乙队在初赛阶段至少要胜5场.
【解析】
试题分析:(1)设甲队胜了x场,则负了(10﹣x)场,根据每队胜一场得2分,负一场得1分,利用甲队在初赛阶段的积分为18分,进而得出等式求出答案;
(2)设乙队在初赛阶段胜a场,根据积分超过15分才能获得参赛资格,进而得出答案.
试题解析:(1)设甲队胜了x场,则负了(10﹣x)场,根据题意可得:
2x+10﹣x=18,
解得:x=8,
则10﹣x=2,
答:甲队胜了8场,则负了2场;
(2)设乙队在初赛阶段胜a场,根据题意可得:
2a+(10﹣a)≥15,
解得:a≥5,
答:乙队在初赛阶段至少要胜5场.

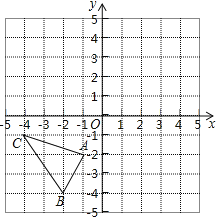
【题目】甲、乙两运动员的射击成绩(靶心为10环)统计如下表(不完全):
次数 运动员 环数 | 1 | 2 | 3 | 4 | 5 |
甲 | 10 | 8 | 9 | 10 | 8 |
乙 | 10 | 9 | 9 | a | b |
某同学计算出了甲的成绩平均数是9,方差是![]() ,请作答:
,请作答:
(1)在图中用折线统计图将甲运动员的成绩表示出来;
(2)若甲、乙的射击成绩平均数都一样,则![]() ;
;
(3)在(2)的条件下,当甲比乙的成绩较稳定时,请列举出![]() 的所有可能取值,并说明理由.
的所有可能取值,并说明理由.

【题目】在开展“经典阅读”活动中,某学校为了解全校学生利用课外时间阅读的情况,学校团委随机抽取若干名学生,调查他们一周的课外阅读时间,并根据调查结果绘制了如下尚不完整的统计表.根据图表信息,解答下列问题:
频率分布表
阅读时间 (小时) | 频数 (人) | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
|
频数分布直方图
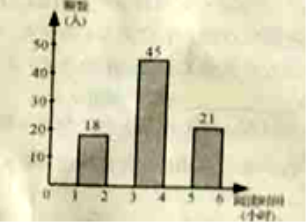
(1)填空:![]() ,
,![]() ,
,![]() ,
,![]() ;
;
(2)将频数分布直方图补充完整(画图后请标注相应的频数);
(3)若该校由![]() 名学生,请根据上述调查结果,估算该校学生一周的课外阅读时间不足三小时的人数.
名学生,请根据上述调查结果,估算该校学生一周的课外阅读时间不足三小时的人数.