ЬтФПФкШн
ЁОЬтФПЁПЁОжЊЪЖЩњГЩЁПЮвУЧвбОжЊЕРЃЌЭЈЙ§МЦЫуМИКЮЭМаЮЕФУцЛ§ПЩвдБэЪОвЛаЉДњЪ§КуЕШЪН.
Р§ШчЭМ![]() ПЩвдЕУЕН
ПЩвдЕУЕН![]() ЃЌЛљгкДЫЃЌЧыНтД№ЯТСаЮЪЬтЃК
ЃЌЛљгкДЫЃЌЧыНтД№ЯТСаЮЪЬтЃК
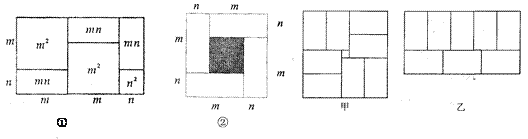
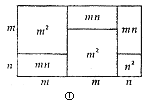
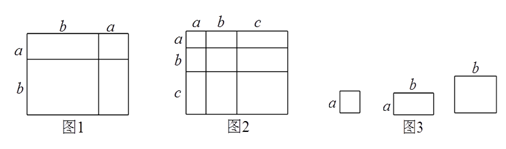
ЃЈ1ЃЉИљОнЭМ2ЃЌаДГівЛИіДњЪ§КуЕШЪНЃК ЃЎ
(2)РћгУЃЈ1ЃЉжаЕУЕНЕФНсТлЃЌНтОіЯТУцЕФЮЪЬтЃКШєa+b+c=10ЃЌab+ac+bc=35ЃЌ![]() = .
= .
(3) аЁУїЭЌбЇгУЭМ жаx еХБпГЄЮЊa ЕФе§ЗНаЮЃЌ yеХБпГЄЮЊb ЕФе§ЗНаЮЃЌz еХПэЁЂГЄЗжБ№ЮЊ aЁЂb ЕФГЄЗНаЮжНЦЌЦДГівЛИіУцЛ§ЮЊ (2a+b)(a+2b)ГЄЗНаЮЃЌдђx+y+z=
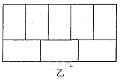
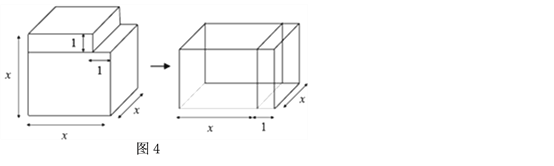
ЁОжЊЪЖЧЈвЦЁПЃЈ4ЃЉЪТЪЕЩЯЃЌЭЈЙ§МЦЫуМИКЮЭМаЮЕФЬхЛ§вВПЩвдБэЪОвЛаЉДњЪ§КуЕШЪНЃЌЭМ4БэЪОЕФЪЧвЛИіБпГЄЮЊ![]() ЕФе§ЗНЬхЭкШЅвЛИіаЁГЄЗНЬхКѓжиаТЦДГЩвЛИіаТГЄЗНЬхЃЌЧыФуИљОнЭМ4жаЭМаЮЕФБфЛЏЙиЯЕЃЌаДГівЛИіДњЪ§КуЕШЪНЃК ЃЎ
ЕФе§ЗНЬхЭкШЅвЛИіаЁГЄЗНЬхКѓжиаТЦДГЩвЛИіаТГЄЗНЬхЃЌЧыФуИљОнЭМ4жаЭМаЮЕФБфЛЏЙиЯЕЃЌаДГівЛИіДњЪ§КуЕШЪНЃК ЃЎ
ЁОД№АИЁП(1)![]() ЃЛ (2) 30ЃЛ (3) 9 ЃЛ
ЃЛ (2) 30ЃЛ (3) 9 ЃЛ
ЃЈ4ЃЉ![]() .
.
ЁОНтЮіЁПЗжЮіЃКЃЈ1ЃЉИљОнЭМ2ЃЌРћгУжБНгЧѓгыМфНгЗЈЗжБ№БэЪОГіе§ЗНаЮУцЛ§ЃЌМДПЩШЗЖЈГіЫљЧѓЕШЪНЃЛ
ЃЈ2ЃЉИљОнЃЈ1ЃЉжаНсЙћЃЌЧѓГіЫљЧѓЪНзгЕФжЕМДПЩЃЛ
ЃЈ3ЃЉИљОнвбжЊЕШЪНЃЌзіГіЯргІЭМаЮЃЌМДПЩЕУЕННсТлЃЛ
ЃЈ4ЃЉЗжБ№БэЪОГіСНИіЭМаЮЕФЬхЛ§ЃЌгЩСНИіЭМаЮЕФЬхЛ§ЯрЕШЃЌМДПЩЕУГіНсТлЃЎ
ЯъНтЃКЃЈ1ЃЉЃЈa+b+cЃЉ2=a2+b2+c2+2ab+2ac+2bcЃЛ
ЃЈ2ЃЉЁпa+b+c=10ЃЌab+bc+ac=35ЃЌЁрa2+b2+c2=ЃЈa+b+cЃЉ2Љ2ЃЈab+ac+bcЃЉ=100Љ70=30ЃЛ
ЃЈ3ЃЉИљОнЬтвтЕУЃКЃЈ2a+bЃЉЃЈa+2bЃЉ=![]() ЃЌЁрx=2ЃЌy=5ЃЌz=2ЃЌЁрx+y+z=9ЃЛ
ЃЌЁрx=2ЃЌy=5ЃЌz=2ЃЌЁрx+y+z=9ЃЛ
ЃЈ4ЃЉЕквЛИіЭМаЮЕФЬхЛ§=![]() ЃЌЕкЖўИіЭМаЮЕФЬхЛ§ЮЊЃК
ЃЌЕкЖўИіЭМаЮЕФЬхЛ§ЮЊЃК![]() ЃЎЁпСНИіЭМаЮЕФЬхЛ§ЯрЕШЃЌЁр
ЃЎЁпСНИіЭМаЮЕФЬхЛ§ЯрЕШЃЌЁр![]() =
=![]() ЃЎ
ЃЎ