题目内容
如图矩形OABC,AB=2OA=2n,分别以OA和OC为x、y轴建立平面直角坐标系,连接OB,沿OB折叠,使点A落在P处.过P作PQ⊥y轴于Q.
(1)求OD:OA的值;
(2)以B为顶点的抛物线:y=ax2+bx+c,经过点D,与直线OB相交于E,过E作EF⊥y轴于F,试判断2•PQ•EF与矩形OABC面积的关系,并说明理由.
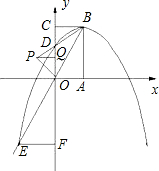
(1)求OD:OA的值;
(2)以B为顶点的抛物线:y=ax2+bx+c,经过点D,与直线OB相交于E,过E作EF⊥y轴于F,试判断2•PQ•EF与矩形OABC面积的关系,并说明理由.

证明:(1)在矩形OABC中AB∥OC,
∴∠ABO=∠BOC,
根据题中的折叠得∠PBO=∠ABO,
∴∠PBO=∠BOC,
∴BD=DO,
设DO=k,则DB=k
在Rt△BCD中BC=n,DC=2n-k,BD=k
∴(2n-k)2+n2=k2,
∴OD=
n,OD:OA=
.
(2)设以B为顶点的抛物线为y=a(x-n)2+2n,
把D(0,n)代入,
得a=
,
∴y=
(x-n)2+2n=
x2+
x+
n,直线OB为y=2x,二者联立,
得E(-
n,-
n),
∴EF=
n,根据PQ⊥y轴于Q,∠BCO=90°,
得△BDC∽△PDQ,通过BD=OD=
n,
得PD=
n,
∴
=
=
=
∴PQ=
n,
∴2•PQ•EF=2n2即矩形OABC面积.
∴∠ABO=∠BOC,
根据题中的折叠得∠PBO=∠ABO,
∴∠PBO=∠BOC,
∴BD=DO,
设DO=k,则DB=k
在Rt△BCD中BC=n,DC=2n-k,BD=k
∴(2n-k)2+n2=k2,
∴OD=
| 5 |
| 4 |
| 5 |
| 4 |
(2)设以B为顶点的抛物线为y=a(x-n)2+2n,
把D(0,n)代入,
得a=
| -3 |
| 4n |
∴y=
| -3 |
| 4n |
| -3 |
| 4n |
| 3 |
| 2 |
| 5 |
| 4 |
得E(-
| 5 |
| 3 |
| 10 |
| 3 |
∴EF=
| 5 |
| 3 |
得△BDC∽△PDQ,通过BD=OD=
| 5 |
| 4 |
得PD=
| 3 |
| 4 |
∴
| PD |
| BD |
| 3 |
| 5 |
| PQ |
| PC |
| PQ |
| n |
∴PQ=
| 3 |
| 5 |
∴2•PQ•EF=2n2即矩形OABC面积.

练习册系列答案
相关题目
 O)的顶点C在直线AB上,以C为圆心,CA的长为半径作⊙C.
O)的顶点C在直线AB上,以C为圆心,CA的长为半径作⊙C.
 门票为每张x元,且40≤x≤70,经市场调研发现一天游览人数y与票价x之间存在着如图所示的一次函数关系.
门票为每张x元,且40≤x≤70,经市场调研发现一天游览人数y与票价x之间存在着如图所示的一次函数关系.