Question

△ABC中，AB=AC，点D为射线BC上一个动点（不与B、C重合），以AD为一边向AD的左侧作△ADE，使AD=AE，∠DAE=∠BAC，过点E作BC的平行线，交直线AB于点F，连接BE．
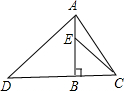
（1）如图1，若∠BAC=∠DAE=60°，则△BEF是______三角形；
（2）若∠BAC=∠DAE≠60°
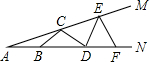
①如图2，当点D在线段BC上移动，判断△BEF的形状并证明；
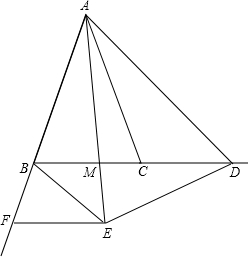
②当点D在线段BC的延长线上移动，△BEF是什么三角形？请直接写出结论并画出相应的图形．

Answer 1

（1）∵AB=AC，AD=AE，∠BAC=∠DAE=60°，
∴△AED和△ABC为等边三角形，
∴∠C=∠ABC=60°，∠EAB=∠DAC，
∴△EAB≌△DAC，
∴∠EBA=∠C=60°，
∵EF∥BC，
∴∠EFB=∠ABC=60°，
∵在△EFB中，∠EFB=∠EBA=60°，
∴△EFB为等边三角形，

（2）①△BEF为等腰三角形，
∵AB=AC，AD=AE，∠BAC=∠DAE，
∴△AED和△ABC为等腰三角形，
∴∠C=∠ABC，∠EAB=∠DAC，
∴△EAB≌△DAC，
∴∠EBA=∠C，
∵EF∥BC，
∴∠EFB=∠ABC，
∵在△EFB中，∠EFB=∠EBA，
∴△EFB为等腰三角形，
②AB=AC，点D为射线BC上一个动点（不与B、C重合），以AD为一边向AD的左侧作△ADE，使AD=AE，∠DAE=∠BAC，过点E作BC的平行线，交直线AB于点F，连接BE．
∵△BEF为等腰三角形，
∵AB=AC，AD=AE，∠BAC=∠DAE，
∴△AED和△ABC为等腰三角形，
∴∠ACB=∠ABC，∠EAB=∠DAC，
∴△EAB≌△DAC，
∴∠EBA=∠ACD，
∴∠EBF=∠ACB，
∵EF∥BC，
∴∠AFE=∠ABC，
∵∠ABC=∠ACB，
∴∠AFE=∠ACB，
∵在△EFB中，∠EBF=∠AFE，
∴△EFB为等腰三角形．