题目内容
等腰△ABC中,AB的中垂线与AC所在直线相交成的锐角为50°,则底角B的大小为______.
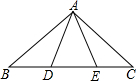
(1)当AB为底边时:∵∠CAD=50°,
∴底角∠A=∠B=90°-50°=40°;
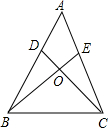
(2)当AB为腰时,且是锐角三角形时,∵ED是AB的中垂线,
∴顶角∠A=90°-50°=40°,
∴底角∠B=
=70°;
(3)当AB为腰,且是钝角三角形时,
∵∠AFG=50°,FG垂直平分AB,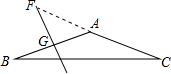
∴∠FAG=90°-50°,
∵AB=AC,
∴∠B=∠C,
∴∠B=
∠FAG=20°.
故底角B的大小为40°或70°或20°.
∴底角∠A=∠B=90°-50°=40°;
(2)当AB为腰时,且是锐角三角形时,∵ED是AB的中垂线,
∴顶角∠A=90°-50°=40°,
∴底角∠B=
| 180°-40° |
| 2 |
(3)当AB为腰,且是钝角三角形时,
∵∠AFG=50°,FG垂直平分AB,

∴∠FAG=90°-50°,
∵AB=AC,
∴∠B=∠C,
∴∠B=
| 1 |
| 2 |
故底角B的大小为40°或70°或20°.


练习册系列答案
相关题目