题目内容
等腰三角形底边与腰上的高的夹角为( )
| A.底角的一半 | B.顶角的一半 |
| C.顶角外角的一半 | D.顶角 |
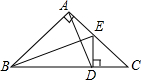
如图(1),
∵AB=AC,BD⊥AC,
∴∠ABD=90°-∠A,∠ABC=∠C=
=90°-
∠A,
∴∠DBC=∠ABC-∠ABD=
∠A,
如图(2),
∵AB=AC,BD⊥AC,
∴∠ABD=90°-∠BAD=90°-(180°-∠A)=∠A-90°,∠ABC=∠C=
=90°-
∠A,
∴∠DBC=∠ABD+∠ABC=
∠A.
综上所述,等腰三角形底边与腰上的高的夹角为顶角的一半.
故选B.
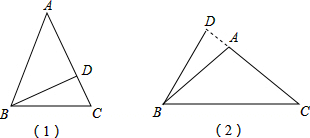
∵AB=AC,BD⊥AC,
∴∠ABD=90°-∠A,∠ABC=∠C=
| 180°-∠A |
| 2 |
| 1 |
| 2 |
∴∠DBC=∠ABC-∠ABD=
| 1 |
| 2 |
如图(2),
∵AB=AC,BD⊥AC,
∴∠ABD=90°-∠BAD=90°-(180°-∠A)=∠A-90°,∠ABC=∠C=
| 180°-∠A |
| 2 |
| 1 |
| 2 |
∴∠DBC=∠ABD+∠ABC=
| 1 |
| 2 |
综上所述,等腰三角形底边与腰上的高的夹角为顶角的一半.
故选B.


练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目