Question

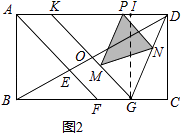
【题目】如图1，在矩形ABCD中，BC＞AB，∠BAD的平分线AF与BD、BC分别交于点E、F，点O是BD的中点，直线OK∥AF，交AD于点K，交BC于点G．

（1）求证：①△DOK≌△BOG；②AB+AK=BG；
（2）若KD=KG，BC=4﹣ ．
①求KD的长度；
②如图2，点P是线段KD上的动点（不与点D、K重合），PM∥DG交KG于点M，PN∥KG交DG于点N，设PD=m，当S△PMN= 时，求m的值．

Answer 1

【答案】
（1）

证明：①∵在矩形ABCD中，AD∥BC

∴∠KDO=∠GBO，∠DKO=∠BGO

∵点O是BD的中点

∴DO=BO

∴△DOK≌△BOG（AAS）

②∵四边形ABCD是矩形

∴∠BAD=∠ABC=90°，AD∥BC

又∵AF平分∠BAD

∴∠BAF=∠BFA=45°

∴AB=BF

∵OK∥AF，AK∥FG

∴四边形AFGK是平行四边形

∴AK=FG

∵BG=BF+FG

∴BG=AB+AK

（2）

解：①由（1）得，四边形AFGK是平行四边形

∴AK=FG，AF=KG

又∵△DOK≌△BOG，且KD=KG

∴AF=KG=KD=BG

设AB=a，则AF=KG=KD=BG= a

∴AK=4﹣ ﹣ a，FG=BG﹣BF= a﹣a

∴4﹣ ﹣ a= a﹣a

解得a=

∴KD= a=2

②过点G作GI⊥KD于点I

由（2）①可知KD=AF=2

∴GI=AB=

∴S△DKG= ×2× =

∵PD=m

∴PK=2﹣m

∵PM∥DG，PN∥KG

∴四边形PMGN是平行四边形，△DKG∽△PKM∽△DPN

∴ ，即S△DPN=（ ）2

同理S△PKM=（ ）2

∵S△PMN=

∴S平行四边形PMGN=2S△PMN=2×

又∵S平行四边形PMGN=S△DKG﹣S△DPN﹣S△PKM

∴2× = ﹣（ ）2 ﹣（ ）2 ，即m2﹣2m+1=0

解得m1=m2=1

∴当S△PMN= 时，m的值为1

【解析】（1）①先根据AAS判定△DOK≌△BOG，②再根据等腰三角形ABF和平行四边形AFKG的性质，得出结论BG=AB+AK；（2）①先根据等量代换得出AF=KG=KD=BG，再设AB=a，根据AK=FG列出关于a的方程，求得a的值，进而计算KD的长；②先过点G作GI⊥KD，求得S△DKG的值，再根据四边形PMGN是平行四边形，以及△DKG∽△PKM∽△DPN，求得S△DPN和S△PKM的表达式，最后根据等量关系S平行四边形PMGN=S△DKG﹣S△DPN﹣S△PKM ， 列出关于m的方程，求得m的值即可．