��Ŀ����
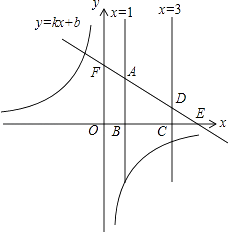
����Ŀ����֪����������y= ![]() ��ͼ���ڶ������ޣ�һ�κ���Ϊy=kx+b��b��0����ֱ��x=1��x�ύ�ڵ�B����ֱ��y=kx+b���ڵ�A��ֱ��x=3��x�ύ�ڵ�C����ֱ��y=kx+b���ڵ�D��
��ͼ���ڶ������ޣ�һ�κ���Ϊy=kx+b��b��0����ֱ��x=1��x�ύ�ڵ�B����ֱ��y=kx+b���ڵ�A��ֱ��x=3��x�ύ�ڵ�C����ֱ��y=kx+b���ڵ�D��
��1������A��D���ڵ�һ���ޣ���֤��b����3k��
��2���ڣ�1���������£���ֱ��y=kx+b��x�ύ�ڵ�E��y�ύ�ڵ�F���� ![]() =
= ![]() �ҡ�OFE���������
�ҡ�OFE��������� ![]() ʱ�������һ�κ����Ľ���ʽ����ֱ��д������ʽ
ʱ�������һ�κ����Ľ���ʽ����ֱ��д������ʽ ![]() ��kx+b�Ľ⼯��
��kx+b�Ľ⼯��
���𰸡�
��1��
֤�����߷���������y= ![]() ��ͼ���ڶ������ޣ�
��ͼ���ڶ������ޣ�
��k��0��
��һ�κ���Ϊy=kx+b��x���������С��
��A��D���ڵ�һ���ޣ�
��3k+b��0��
��b����3k
��2��
�⣺������֪�� ![]() ��
��
�� ![]() �٣�
�٣�
��E���� ![]() ��0����F��0��b����
��0����F��0��b����
��S��OEF= ![]() ������
������ ![]() ����b=
����b= ![]() �ڣ�
�ڣ�
�ɢ٢������������ã�k=�� ![]() ��b=3��
��b=3��
�����һ�κ����Ľ���ʽΪy=�� ![]() x+3��
x+3��
�⩁ ![]() =��
=�� ![]() x+3��x1=
x+3��x1= ![]() ��x2=
��x2= ![]() ��
��
��ֱ��y=kx+b�뷴��������y= ![]() �Ľ�������ĺ�������
�Ľ�������ĺ������� ![]() ��
�� ![]() ��
��
���ʽ ![]() ��kx+b�Ľ⼯Ϊ
��kx+b�Ľ⼯Ϊ ![]() ��x��0��x��
��x��0��x�� ![]() ��
��
����������1���ɷ���������y= ![]() ��ͼ���ڶ������ޣ��õ�k��0�����ǵõ�һ�κ���Ϊy=kx+b��x���������С������A��D���ڵ�һ���ޣ��õ�����ʽ���ɵõ����ۣ���2����������õ�
��ͼ���ڶ������ޣ��õ�k��0�����ǵõ�һ�κ���Ϊy=kx+b��x���������С������A��D���ڵ�һ���ޣ��õ�����ʽ���ɵõ����ۣ���2����������õ� ![]() ���������ε������ʽ�õ�S��OEF=
���������ε������ʽ�õ�S��OEF= ![]() ������
������ ![]() ����b=
����b= ![]() ������������k=��
������������k=�� ![]() ��b=3�����ɵõ����ۣ�
��b=3�����ɵõ����ۣ�







