Question

【题目】如图，“中国海监50”正在南海海域A处巡逻，岛礁B上的中国海军发现点A在点B的正西方向上，岛礁C上的中国海军发现点A在点C的南偏东30°方向上，已知点C在点B的北偏西60°方向上，且B、C两地相距120海里．

（1）求出此时点A到岛礁C的距离；
（2）若“中海监50”从A处沿AC方向向岛礁C驶去，当到达点A′时，测得点B在A′的南偏东75°的方向上，求此时“中国海监50”的航行距离．（注：结果保留根号）

Answer 1

【答案】
（1）

解：如图所示：

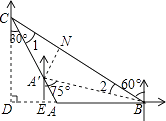
延长BA，过点C作CD⊥BA延长线与点D，

由题意可得：∠CBD=30°，BC=120海里，

则DC=60海里，

故cos30°= = = ，

解得：AC=40 ，

答：点A到岛礁C的距离为40 海里

（2）

解：如图所示：

过点A′作A′N⊥BC于点N，

可得∠1=30°，∠BA′A=45°，A′N=A′E，

则∠2=15°，即A′B平分∠CBA，

设AA′=x，则A′E= x，

故CA′=2A′N=2× x= x，

∵ x+x=40 ，

∴解得：x=60﹣20 ，

答：此时“中国海监50”的航行距离为（60﹣20 ）海里．

【解析】（1）根据题意得出：∠CBD=30°，BC=120海里，再利用cos30°= ，进而求出答案；（2）根据题意结合已知得出当点B在A′的南偏东75°的方向上，则A′B平分∠CBA，进而得出等式求出答案．